Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
Риманово многообразие, или риманово пространство (M, g), — это (вещественное) гладкое многообразие M, в котором каждое касательное пространство снабжено скалярным произведением g — метрическим тензором, меняющимся от точки к точке гладким образом. Другими словами, риманово многообразие — это дифференцируемое многообразие, в котором касательное пространство в каждой точке является конечномерным евклидовым пространством.
Сплайн — функция в математике, область определения которой разбита на конечное число отрезков, на каждом из которых она совпадает с некоторым алгебраическим многочленом (полиномом). Максимальная из степеней использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1. В современном понимании сплайны — это решения многоточечных краевых задач сеточными методами.
Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий заданные значения в заданном наборе точек, то есть решающий задачу интерполяции.
Кривы́е Безье́ или Кривы́е Бернште́йна — Безье́ — типы кривых, предложенные в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Лине́йная комбина́ция — выражение, построенное на множестве элементов путём умножения каждого элемента на коэффициенты с последующим сложением результатов.
Кубический сплайн — гладкая функция, область определения которой разбита на конечное число отрезков, на каждом из которых она совпадает с некоторым кубическим многочленом (полиномом).
Гра́фик фу́нкции — геометрическое понятие в математике, дающее представление о геометрическом образе функции.
Поверхность Безье — параметрическая поверхность, используемая в компьютерной графике, автоматизированном проектировании, и моделировании. Это одно из распространённых пространственных обобщений кривой Безье.
Моносплайн — вид сплайна, сконструированный из степенной функции 
и полиномиального сплайна степени 
, получивший распространение в задачах поиска наилучших квадратурных формул для дифференцируемых функций и ряде других приложений; считаются удобными для компьютерных реализаций.
В вычислительной математике многочлены Бернштейна — это алгебраические многочлены, представляющие собой линейную комбинацию базисных многочленов Бернштейна.
Тео́рия автомати́ческого управле́ния (ТАУ) — научная дисциплина, которая изучает процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию.
В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов
,
Сглаживающий сплайн это метод сглаживания с использованием сплайн-функций.
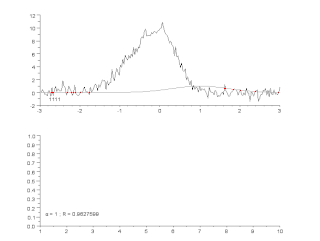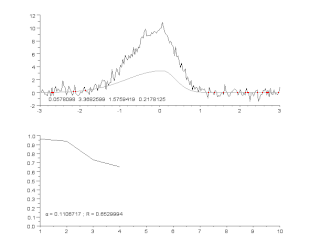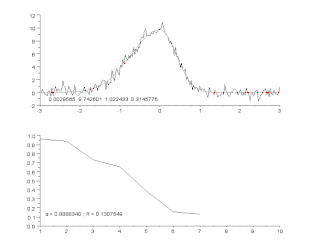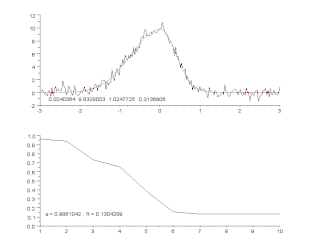
Приближение с помощью кривых — это процесс построения кривой или математической функции, которая наилучшим образом приближается к заданным точкам с возможными ограничениями на кривую. Для построения такого приближения может использоваться либо интерполяция, где требуется точное прохождение кривой через точки, либо сглаживание, когда «сглаживающая» функция проходит через точки приближённо. Связанный раздел — регрессионный анализ, который фокусируется, главным образом, на вопросах статистического вывода, таких как, какая неопределённость заключена в кривой, которая приближает данные с некоторыми случайными ошибками. Построенные кривые могут быть использованы для визуализации данных, для вычисления значений функции в точках, в которых значение не задано и для определения связи между двумя и более переменными. Экстраполяция означает использование полученной кривой за пределами данных, полученных из наблюдения, и порождает некоторую неопределённость, поскольку может зависеть от метода построения кривой.
Подпись при обучении с ошибками в кольце — один из классов криптосистем с открытым ключом, основанный на задаче обучения с ошибками в кольце, который заменяет используемые алгоритмы подписи RSA и ECDSA. В течение последнего десятилетия проводились активные исследования по созданию криптографических алгоритмов, которые остаются безопасными, даже если у злоумышленника есть ресурсы квантового компьютера. Подпись при обучении с ошибками в кольце относится к числу пост-квантовых подписей с наименьшим открытым ключом и размерами подписи. Использование общей проблемы обучения с ошибками в криптографии было введено Одедом Регевым в 2005 году и послужило источником нескольких криптографических разработок. Основоположники криптографии при обучении с ошибками в кольце, считают, что особенностью этих алгоритмов, основанных на обучении с ошибками, является доказуемое сокращение известных сложных задач. Данная подпись имеет доказуемое сокращение до задачи нахождения кратчайшего вектора в области криптографии на решётках. Это означает, что если можно обнаружить атаку на криптосистему RLWE, то целый класс предполагаемых сложных вычислительных проблем будет иметь решение. Первая подпись на основе RLWE была разработана Вадимом Любашевским и уточнена в 2011 году. Данная статья освещает фундаментальные математические основы RLWE и основана на схеме под названием GLYPH.
Алгоритм де Бура — это численный метод вычисления значения B-сплайна в заданной точке; является обобщением алгоритма де Кастельжо для кривых Безье. Оригинальная версия алгоритма, разработанная Карлом де Буром в 1971 году, имеет полиномиальную вычислительную сложность, но отличается хорошей численной устойчивостью. Последующие модификации, появившиеся в попытке упростить и ускорить алгоритм, демонстрируют сравнительно худшую устойчивость.
