Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре.
Алгоритм Хаффмана — жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.
Алгори́тм Де́йкстры — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании, например, его используют протоколы маршрутизации OSPF и IS-IS.
Суффиксное дерево — бор, содержащий все суффиксы некоторой строки. Позволяет выяснять, входит ли строка w в исходную строку t, за время O(|w|), где |w| — длина строки w.
Метод ветвей и границ — общий алгоритмический метод для нахождения оптимальных решений различных задач оптимизации, особенно дискретной и комбинаторной оптимизации. Метод является развитием метода полного перебора, в отличие от последнего — с отсевом подмножеств допустимых решений, заведомо не содержащих оптимальных решений.
Префиксное дерево — структура данных, позволяющая хранить ассоциативный массив, ключами которого чаще всего являются строки. Представляет собой корневое дерево, каждое ребро которого помечено каким-то символом так, что для любого узла все рёбра, соединяющие этот узел с его сыновьями, помечены разными символами. Некоторые узлы префиксного дерева выделены и считается, что префиксное дерево содержит данную строку-ключ тогда и только тогда, когда эту строку можно прочитать на пути из корня до некоторого выделенного узла. В некоторых приложениях удобно считать все узлы дерева выделенными.
Двоичное дерево поиска — двоичное дерево, для которого выполняются следующие дополнительные условия :
- оба поддерева — левое и правое — являются двоичными деревьями поиска;
- у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X;
- у всех узлов правого поддерева произвольного узла X значения ключей данных больше либо равны, нежели значение ключа данных самого узла X.
Дерево принятия решений — средство поддержки принятия решений, использующееся в машинном обучении, анализе данных и статистике. Структура дерева представляет собой «листья» и «ветки». На рёбрах («ветках») дерева решения записаны признаки, от которых зависит целевая функция, в «листьях» записаны значения целевой функции, а в остальных узлах — признаки, по которым различаются случаи. Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение.
B-дерево — структура данных, дерево поиска. С точки зрения внешнего логического представления, сбалансированное, сильно ветвистое дерево во внешней памяти.
Задача целочисленного программирования — это задача математической оптимизации или выполнимости, в которой некоторые или все переменные должны быть целыми числами. Часто термин адресуется к целочисленному линейному программированию (ЦЛП), в котором целевая функция и ограничения линейны.
Метод золотого сечения — метод поиска экстремума действительной функции одной переменной на заданном отрезке. В основе метода лежит принцип деления отрезка в пропорциях золотого сечения. Является одним из простейших вычислительных методов решения задач оптимизации. Впервые представлен Джеком Кифером в 1953 году.
Обучение на примерах — вид обучения, при котором интеллектуальной системе предъявляется набор положительных и отрицательных примеров, связанных с какой-либо заранее неизвестной закономерностью. В интеллектуальных системах вырабатываются решающие правила, с помощью которых происходит разделение множества примеров на положительные и отрицательные. Качество разделения, как правило, проверяется экзаменационной выборкой примеров.
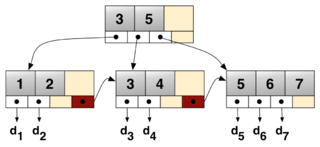
B⁺-дерево — структура данных на основе B-дерева, сбалансированное 
-арное дерево поиска с переменным, но зачастую большим количеством потомков в узле. B⁺-дерево состоит из корня, внутренних узлов и листьев, корень может быть либо листом, либо узлом с двумя и более потомками.
Криптографическая хеш-функция — всякая хеш-функция, являющаяся криптостойкой, то есть удовлетворяющая ряду требований, специфичных для криптографических приложений.
C4.5 — алгоритм для построения деревьев решений, разработанный Джоном Квинланом. C4.5 является усовершенствованной версией алгоритма ID3 того же автора. В частности, в новую версию были добавлены отсечение ветвей, возможность работы с числовыми атрибутами, а также возможность построения дерева из неполной обучающей выборки, в которой отсутствуют значения некоторых атрибутов.
В теории графов древесная декомпозиция — это отображение графа в дерево, которое может быть использовано для определения древесной ширины графа и ускорения решения определённых вычислительных задач на графах.
Отбор признаков — процесс отбора подмножества значимых признаков для построения модели в машинном обучении. Отбор признаков используется по четырём причинам:
- упрощение модели для повышения интерпретируемости
- для сокращения времени обучения
- во избежание проклятия размерности
- улучшение обобщающей способности модели и борьба с переобучением.
Обучение дерева решений использует дерево решений, чтобы перейти от наблюдений над объектами к заключениям о целевых значениях объектов. Это обучение является одним из подходов моделирования предсказаний, используемых в статистике, интеллектуальном анализе данных и машинном обучении. Модели деревьев, в которых целевая переменная может принимать дискретный набор значений, называются деревьями классификации. В этих структурах деревьев листья представляют метки классов, а ветки представляют конъюнкции признаков, которые ведут в эти метки классов. Деревья решений, в которых целевая переменная может принимать непрерывные значения называются деревьями регрессии.
Минимально критичное остовное дерево во взвешенном неориентированном графе — это остовное дерево, в котором наиболее тяжёлое ребро весит как можно меньше. Критичное ребро — это самое тяжёлое ребро в стягивающем дереве. Стягивающее дерево является минимальным критичным остовным деревом, если граф не содержит стягивающего дерева с критичным ребром меньшего веса. Для ориентированного графа аналогичная задача известна как минимально критичное стягивающее ориентированное дерево.
