JH

JH
JH
Разработчики	У Хунцзюнь (англ Wu Hongjun)
Опубликован	16 января 2011 года
Размер хеша	224, 256, 384, 512
Число раундов	42

JH — семейство из четырёх криптографических хеш-функций: JH-224, JH-256, JH-384 и JH-512.

Алгоритмы этих хеш-функций отличаются только значением одного внутреннего параметра — длины (в битах) $l_{hash}$ выходного значения (которая и указана после дефиса в названии). Далее в статье при описании алгоритма я буду считать этот параметр частью входных данных для удобства, говоря о JH, как об одном алгоритме или одной хеш-функции.

Хеш-функция JH входит в пятёрку финалистов второго тура SHA-3. В процессе этого конкурса она была улучшена. В статье рассматривается последняя на данный момент версия, которую также можно назвать JH42 (так как главное изменение состояло в том, что число раундов в функции компрессии стало равно 42). Дата выхода документации по ней — 16 января 2011 года.

При хешировании входное сообщение дополняется и разделяется на части, которые далее последовательно обрабатываются так называемой функцией компрессии. Эта функция описана в спецификации в общем виде — то есть с переменным параметром d, меняя который можно конструировать JH-подобные хеш-функции (тем более криптостойкие, чем больше d). В JH исходно d=8.

При выборе финалиста в конкурсе SHA решающую роль играют не криптографические характеристики (они у всех функций отличные), а гибкость и оптимальность в программной и аппаратной реализации. На тему аппаратной реализации существует много исследований, например^[1].

Алгоритм^[2]

Уточнения

О названии элементов битовых векторов

Будем считать, что у всех обсуждаемых тут битовых векторов есть начало и конец, причём бит, расположенный в начале (слева) является первым, имеет позицию 0 и считается наиболее значимым, соответственно, бит, расположенный в конце (справа), является последним, имеет позицию с наибольшим номером, на один меньшим, чем число разрядов вектора, и считается наименее значимым.

То же самое, за исключением номера позиции, будем подразумевать для векторов, состоящих из битовых векторов, например, для сообщения, состоящего из блоков, или блока, состоящего из полубайтов. С номером же позиции какой-либо составной части битового вектора, состоящей из нескольких бит, будет путаница, создаваемая для удобства. Так, номера позиций полубайтов в блоке будут начинаться с нуля, а номера позиций блоков в сообщении — с единицы…

Пример

В векторе

8afd4h

первый, наиболее значимый полубайт расположен слева – это 8; последний, наименее значимый полубайт расположен справа – это 4.

Если эту запись рассматривать, как битовый вектор, а не как полубайтовый, то она эквивалентна такой:

1000_1010_1111_1101_0100,

тут первый(с номером 0, левый, старший) бит - 1, а последний(с номером 19, правый, младший) - 0.

Обозначение конкатенации

Пусть вектор $A$ состоит из последовательно идущих векторов $A_{1},A_{2},\dots ,A_{N}$ , тогда этот факт будет обозначаться так: $A=A_{1}||A_{2}||\dots ||A_{N}$

Используемые функции — обобщённый случай

Здесь описаны функции, с помощью которых можно строить JH-подобные алгоритмы, меняя параметр $d$

S-box — S_i(x)

Это функция, преобразующая s-блок (то есть размеры её входного и выходного значений одинаковы и равны 4 битам). В алгоритме используются 2 таких функции: $S_{1}$ и $S_{0}$ . Их таблицы значений такие:

$x$	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
$S_{0}(x)$	9	0	4	b	d	c	3	f	1	a	2	6	7	5	8	e
$S_{1}(x)$	3	c	6	d	5	7	1	9	f	2	0	4	b	a	e	8

Линейное преобразование пар ячеек — L(A,B)

Эта функция преобразует пару s-блоков (то есть размеры её входного и выходного значений одинаковы и равны 8 битам). Наиболее лаконичную запись она имеет в терминах конечных полей многочленов.

Рассмотрим конечное поле многочленов над $GF(2)$ степени не выше 3-й. Оно изоморфно полю $GF(2^{4})$ ; установим стандартное для таких случаев соответствие межу полем многочленов и полем чисел: многочлен будет соответствовать числу, равному значению многочлена при $x=2$ . Выберем для этого поля многочленов следующий примитивный многочлен:

$x^{4}+x+1$ .

Тогда, если рассматривать $L(A,B)$ , как функцию, преобразующую 2 многочлена, а числа и буквы — как многочлены, то

$L(A,B)=((5\bullet A+2\bullet B),(2\bullet A+B))$ ,

где « $\bullet$ » и « $+$ » — операции умножения и сложения в данном поле многочленов.

Перемешивание — P_d

Функция $P_{d}$ является композицией трёх более простых перемешиваний, преобразующих массив из $2^{d}$ битовых векторов (то есть размеры их входных и выходных значений одинаковы и равны $2^{d}\times k$ битам, где $k$ — число бит в одном элементе этого массива):

$P_{d}(A)=\phi _{d}(P'_{d}(\pi _{d}(A)))$

Приведем алгоритмы этих перемешиваний, обозначив за $A=A_{0}||A_{1}||\dots ||A_{2^{d}-1}$ и $B=B_{0}||B_{1}||\dots ||B_{2^{d}-1}$ (где $A_{i}$ и $B_{i}$ — битовые векторы одинакового размера для всех $i$ ) — входной и выходной векторы соответственно:

$B=\pi _{d}(A)$ :

for~i=0~~to~2^{d-2}-1~~begin

B_{4i+0}=A_{4i+0}

B_{4i+1}=A_{4i+1}

B_{4i+2}=A_{4i+3}

B_{4i+3}=A_{4i+2}

end

$B=P'_{d}(A)$ :

for~i=0~~to~2^{d-1}-1~~begin

B_{i}=A_{2i}

B_{i+2^{d-1}}=A_{2i+1}

end

$B=\phi _{d}(A)$ :

for~i=0~~to~2^{d-2}-1~~begin

B_{2i}=A_{2i}

B_{2i+1}=A_{2i+1}

B_{2^{d-1}+2i}=A_{2^{d-1}+2i+1}

B_{2^{d-1}+2i+1}=A_{2^{d-1}+2i}

end

Преобразование-раунд — R_d(A,C)

На вход подается $2^{d+2}$ - мерный вектор $A$ . Выход — $2^{d+2}$ - мерный вектор. Так же на вход подается $2^{d}$ -битная константа $C$ .

Вектор $A$ представляется в виде массива из $2^{d}$ полубайт: $A=A_{0}||A_{1}||\dots ||A_{2^{d}-1}$ .

Потом над каждым полубайтом $A_{i}$ производится преобразование $S_{0}$ или $S_{1}$ в зависимости от значения $C_{i}$ (если $C_{i}=0$ , то $S_{0}$ , иначе — $S_{1}$ )

Далее над каждой парой вида $(S_{C_{2i}}(A_{2i}),S_{C_{2i+1}}(A_{2i+1}))$ производится линейное преобразование $L(S_{C_{2i}}(A_{2i}),S_{C_{2i+1}}(A_{2i+1}))$ .

И в конце концов результаты опять группируются в вектор, биты которого подвергаются перемешиванию $P_{d}$ .

Это выражается в виде формулы:

$R_{d}(A,C)=P_{d}{\bigg (}L{\Big (}S_{C_{0}}(A_{0}),S_{C_{1}}(A_{1}){\Big )}||L{\Big (}S_{C_{2}}(A_{2}),S_{C_{3}}(A_{3}){\Big )}||\dots ||L{\Big (}S_{C_{2^{d}-2}}(A_{2^{d}-2}),S_{C_{2^{d}-1}}(A_{2^{d}-1}){\Big )}{\bigg )}$

Преобразование E_d

На входе $2^{d+2}$ — мерный вектор $A$ . Сначала происходит начальная группировка:

$B=G_{d}(A)$ :

for~i=0~~to~2^{d-1}-1~~begin

B_{8i+0}=A_{i+128\times 0}

B_{8i+1}=A_{i+128\times 2}

B_{8i+2}=A_{i+128\times 4}

B_{8i+3}=A_{i+128\times 6}

B_{8i+4}=A_{i+128\times 1}

B_{8i+5}=A_{i+128\times 3}

B_{8i+6}=A_{i+128\times 5}

B_{8i+7}=A_{i+128\times 7}

end

Далее к результату $B$ этой группировки применяется $6\times (d-1)$ преобразований-раундов $R_{d}(B,C)$ с константами, изменяющимися от раунда к раунду. Начальное значение переменной $C$ задаётся, как целая часть числа $({\sqrt {2}}-1)\times 2^{2^{d}}$ , то есть

$C=\left\lfloor ({\sqrt {2}}-1)\times 2^{2^{d}}\right\rfloor$ :

for~i=1~~to~6\times (d-1)~~begin

C=R_{d-2}(C,0)

B=R_{d}(B,C)

end

Далее происходит конечная разгруппировка, обратная начальной:

$B_{fin}=G_{d}^{-1}(B)$ ,

Где $G_{d}^{-1}:G_{d}(G_{d}^{-1}(B))\equiv B$

В виде псевдокода:

$B_{fin}=G_{d}^{-1}(B)$ :

for~i=0~~to~2^{d-1}-1~~begin

B_{fin~i+128\times 0}=B_{8i+0}

B_{fin~i+128\times 2}=B_{8i+1}

B_{fin~i+128\times 4}=B_{8i+2}

B_{fin~i+128\times 6}=B_{8i+3}

B_{fin~i+128\times 1}=B_{8i+4}

B_{fin~i+128\times 3}=B_{8i+5}

B_{fin~i+128\times 5}=B_{8i+6}

B_{fin~i+128\times 7}=B_{8i+7}

end

Таким образом,

$E_{d}(A)=G^{-1}(R_{d}(R_{d}(R_{d}(\dots (R_{d}(G_{d}(A)),C_{1})\dots ),C_{6(d-1)-1}),C_{6(d-1)}))$

$C_{i}=R_{d-2}(C_{i-1},0),~i=1\dots 6(d-1),~C_{0}=\left\lfloor ({\sqrt {2}}-1)\times 2^{2^{d}}\right\rfloor$

Функция свёртки F_d(H,M)

На входе $2^{d+2}$ -битный вектор $H$ и $2^{d+1}$ -битный вектор $M$ . Сначала $H$ преобразуется путём побитового сложения первой половины этого вектора с $M$ , потом над результатом выполняется преобразование $E_{d}$ и наконец результат преобразуется путём побитового сложения его второй половины с вектором $M$ .

Запишем это в виде формул. Пусть $H_{left}$ — первая (старшая) половина вектора $H$ , а $H_{right}$ — вторая. Пусть также функции $E_{d-left}(A)$ и $E_{d-right}(A)$ возвращают левую и правую половины $E_{d}(A)$ соответственно. Тогда

$F_{d}(H,M)=E_{d-left}{\Big (}(H_{left}\oplus M)||H_{right}{\Big )}||{\bigg (}E_{d-right}{\Big (}(H_{left}\oplus M)||H_{right}{\Big )}\oplus M{\bigg )}$

Используемые функции — адаптация к аппаратной реализации при d=8

Конкретная реализация во многом зависит от таких параметров, как

Желательное быстродействие
Желательный размер
Желательная технология
Желательное энергопотребление
Желательная помехоустойчивость
Желательная стоимость

Поэтому без задания этих параметров адаптация невозможна. Я дам описание преобразования $L$ с помощью обычных для аппаратной разработки побитовых операций, а также некоторые константы, которые могут пригодиться, если нет существенного ограничения по размерам схемы.

Выражение преобразования L через простые операции с битами

Пусть $L(A,B)=C_{0}||C_{1}||C_{2}||C_{3}||D_{0}||D_{1}||D_{2}||D_{3},$ , тогда

$D_{0}=B_{0}\oplus A_{1};$

$D_{1}=B_{1}\oplus A_{2};$

$D_{2}=B_{2}\oplus A_{3}\oplus A_{0};$

$D_{3}=B_{3}\oplus A_{0};$

$C_{0}=A_{0}\oplus D_{1};$

$C_{1}=A_{1}\oplus D_{2};$

$C_{2}=A_{2}\oplus D_{3}\oplus D_{0};$

$C_{3}=A_{3}\oplus D_{0}.$

где « $\oplus$ » — операция «исключающее или».

Пусть входной и выходной векторы lin_trans_in[0:7] и lin_trans_out[0:7] соответственно, тогда

verilog-код

assign 
lin_trans_out[4:7]=lin_trans_in[4:7] ^ {lin_trans_in [1:3],lin_trans_in [0]} ^ {2'b0,lin_trans_in [0],1'b0},
lin_trans_out[0:3]=lin_trans_in[0:3] ^ {lin_trans_out[1:3],lin_trans_out[0]} ^ {2'b0,lin_trans_out[0],1'b0};

Константы H₀ при разных l_hash

Для $l_{hash}=~512,~384,~256,~224$ будем иметь соответственно:

verilog-код

assign 
hash_0_512[0:1023]= 1024'h6fd14b963e00aa17636a2e057a15d5438a225e8d0c97ef0be9341259f2b3c361891da0c1536f801e2aa9056bea2b6d80588eccdb2075baa6a90f3a76baf83bf70169e60541e34a6946b58a8e2e6fe65a1047a7d0c1843c243b6e71b12d5ac199cf57f6ec9db1f856a706887c5716b156e3c2fcdfe68517fb545a4678cc8cdd4b,
hash_0_384[0:1023]= 1024'h481e3bc6d813398a6d3b5e894ade879b63faea68d480ad2e3324cb21480f826798aec84d9082b928d45dea304111424936f555b2924847ecc72d0a93baf43ce1569b7f8a27db454c9ef4bd496397af0e589fc27d26aa80cd80c88b8c9deb2eda8a7981e8f8d5373af43967adddd17a71a9b4d3bda475d39497643fba9842737f,
hash_0_256[0:1023]= 1024'heb98a3412c20d3eb92cdbe7b9cb245c11c93519160d4c7fa260082d67e508a03a4239e267726b945e0fb1a48d41a9477cdb5ab26026b177a56f024420fff2fa871a396897f2e4d751d144908f77de262277695f776248f9487d5b6574780296c5c5e272dac8e0d6c518450c657057a0f7be4d367702412ea89e3ab13d31cd769,
hash_0_224[0:1023]= 1024'h2dfedd62f99a98acae7cacd619d634e7a4831005bc301216b86038c6c966149466d9899f2580706fce9ea31b1d9b1adc11e8325f7b366e10f994857f02fa06c11b4f1b5cd8c840b397f6a17f6e738099dcdf93a5adeaa3d3a431e8dec9539a6822b4a98aec86a1e4d574ac959ce56cf015960deab5ab2bbf9611dcf0dd64ea6e;

Константы C раундов R₈

$C_{i}=R_{6}(C_{i-1},0),~i=1\dots 42,~C_{0}=\left\lfloor ({\sqrt {2}}-1)\times 2^{256}\right\rfloor$

Представим их в виде массива, $C_{i+1}=$ round_const[i][0:255]

verilog-код

assign 
round_const[0 ][0:255]=256'h6a09e667f3bcc908b2fb1366ea957d3e3adec17512775099da2f590b0667322a,
round_const[1 ][0:255]=256'hbb896bf05955abcd5281828d66e7d99ac4203494f89bf12817deb43288712231,
round_const[2 ][0:255]=256'h1836e76b12d79c55118a1139d2417df52a2021225ff6350063d88e5f1f91631c,
round_const[3 ][0:255]=256'h263085a7000fa9c3317c6ca8ab65f7a7713cf4201060ce886af855a90d6a4eed,
round_const[4 ][0:255]=256'h1cebafd51a156aeb62a11fb3be2e14f60b7e48de85814270fd62e97614d7b441,
round_const[5 ][0:255]=256'he5564cb574f7e09c75e2e244929e9549279ab224a28e445d57185e7d7a09fdc1,
round_const[6 ][0:255]=256'h5820f0f0d764cff3a5552a5e41a82b9eff6ee0aa615773bb07e8603424c3cf8a,
round_const[7 ][0:255]=256'hb126fb741733c5bfcef6f43a62e8e5706a26656028aa897ec1ea4616ce8fd510,
round_const[8 ][0:255]=256'hdbf0de32bca77254bb4f562581a3bc991cf94f225652c27f14eae958ae6aa616,
round_const[9 ][0:255]=256'he6113be617f45f3de53cff03919a94c32c927b093ac8f23b47f7189aadb9bc67,
round_const[10][0:255]=256'h80d0d26052ca45d593ab5fb3102506390083afb5ffe107dacfcba7dbe601a12b,
round_const[11][0:255]=256'h43af1c76126714dfa950c368787c81ae3beecf956c85c962086ae16e40ebb0b4,
round_const[12][0:255]=256'h9aee8994d2d74a5cdb7b1ef294eed5c1520724dd8ed58c92d3f0e174b0c32045,
round_const[13][0:255]=256'h0b2aa58ceb3bdb9e1eef66b376e0c565d5d8fe7bacb8da866f859ac521f3d571,
round_const[14][0:255]=256'h7a1523ef3d970a3a9b0b4d610e02749d37b8d57c1885fe4206a7f338e8356866,
round_const[15][0:255]=256'h2c2db8f7876685f2cd9a2e0ddb64c9d5bf13905371fc39e0fa86e1477234a297,
round_const[16][0:255]=256'h9df085eb2544ebf62b50686a71e6e828dfed9dbe0b106c9452ceddff3d138990,
round_const[17][0:255]=256'he6e5c42cb2d460c9d6e4791a1681bb2e222e54558eb78d5244e217d1bfcf5058,
round_const[18][0:255]=256'h8f1f57e44e126210f00763ff57da208a5093b8ff7947534a4c260a17642f72b2,
round_const[19][0:255]=256'hae4ef4792ea148608cf116cb2bff66e8fc74811266cd641112cd17801ed38b59,
round_const[20][0:255]=256'h91a744efbf68b192d0549b608bdb3191fc12a0e83543cec5f882250b244f78e4,
round_const[21][0:255]=256'h4b5d27d3368f9c17d4b2a2b216c7e74e7714d2cc03e1e44588cd9936de74357c,
round_const[22][0:255]=256'h0ea17cafb8286131bda9e3757b3610aa3f77a6d0575053fc926eea7e237df289,
round_const[23][0:255]=256'h848af9f57eb1a616e2c342c8cea528b8a95a5d16d9d87be9bb3784d0c351c32b,
round_const[24][0:255]=256'hc0435cc3654fb85dd9335ba91ac3dbde1f85d567d7ad16f9de6e009bca3f95b5,
round_const[25][0:255]=256'h927547fe5e5e45e2fe99f1651ea1cbf097dc3a3d40ddd21cee260543c288ec6b,
round_const[26][0:255]=256'hc117a3770d3a34469d50dfa7db020300d306a365374fa828c8b780ee1b9d7a34,
round_const[27][0:255]=256'h8ff2178ae2dbe5e872fac789a34bc228debf54a882743caad14f3a550fdbe68f,
round_const[28][0:255]=256'habd06c52ed58ff091205d0f627574c8cbc1fe7cf79210f5a2286f6e23a27efa0,
round_const[29][0:255]=256'h631f4acb8d3ca4253e301849f157571d3211b6c1045347befb7c77df3c6ca7bd,
round_const[30][0:255]=256'hae88f2342c23344590be2014fab4f179fd4bf7c90db14fa4018fcce689d2127b,
round_const[31][0:255]=256'h93b89385546d71379fe41c39bc602e8b7c8b2f78ee914d1f0af0d437a189a8a4,
round_const[32][0:255]=256'h1d1e036abeef3f44848cd76ef6baa889fcec56cd7967eb909a464bfc23c72435,
round_const[33][0:255]=256'ha8e4ede4c5fe5e88d4fb192e0a0821e935ba145bbfc59c2508282755a5df53a5,
round_const[34][0:255]=256'h8e4e37a3b970f079ae9d22a499a714c875760273f74a9398995d32c05027d810,
round_const[35][0:255]=256'h61cfa42792f93b9fde36eb163e978709fafa7616ec3c7dad0135806c3d91a21b,
round_const[36][0:255]=256'hf037c5d91623288b7d0302c1b941b72676a943b372659dcd7d6ef408a11b40c0,
round_const[37][0:255]=256'h2a306354ca3ea90b0e97eaebcea0a6d7c6522399e885c613de824922c892c490,
round_const[38][0:255]=256'h3ca6cdd788a5bdc5ef2dceeb16bca31e0a0d2c7e9921b6f71d33e25dd2f3cf53,
round_const[39][0:255]=256'hf72578721db56bf8f49538b0ae6ea470c2fb1339dd26333f135f7def45376ec0,
round_const[40][0:255]=256'he449a03eab359e34095f8b4b55cd7ac7c0ec6510f2c4cc79fa6b1fee6b18c59e,
round_const[41][0:255]=256'h73bd6978c59f2b219449b36770fb313fbe2da28f6b04275f071a1b193dde2072;

Позиции полубайтов после перемешивания P₈

Пусть на вход $P_{8}$ поступил 1024-битный вектор — массив из 256-ти 4-битных векторов: $A=A_{1}||A_{2}||\dots ||A_{256}$ , а на выходе имеем $B=B_{1}||B_{2}||\dots ||B_{256}$ , тогда $B_{i}=A_{permut\_pose[i*8-1-:8]}$ . Это означает, что первый полубайт выходного вектора $B$ будет равен полубайту входного вектора $A$ с номером позиции (от 0 до 255), содержащемся в первом байте константы permut_pose[0:2047], второй полубайт выходного вектора — полубайту входного вектора с номером позиции, содержащемся во втором байте permut_pose[0:2047], и т. д.

verilog-код

assign 
permut_pose[0:2047]=2048'h00030407080b0c0f10131417181b1c1f20232427282b2c2f30333437383b3c3f40434447484b4c4f50535457585b5c5f60636467686b6c6f70737477787b7c7f80838487888b8c8f90939497989b9c9fa0a3a4a7a8abacafb0b3b4b7b8bbbcbfc0c3c4c7c8cbcccfd0d3d4d7d8dbdcdfe0e3e4e7e8ebeceff0f3f4f7f8fbfcff020106050a090e0d121116151a191e1d222126252a292e2d323136353a393e3d424146454a494e4d525156555a595e5d626166656a696e6d727176757a797e7d828186858a898e8d929196959a999e9da2a1a6a5aaa9aeadb2b1b6b5bab9bebdc2c1c6c5cac9cecdd2d1d6d5dad9dedde2e1e6e5eae9eeedf2f1f6f5faf9fefd;

Используемые функции — адаптация к программной реализации при d=8

Суть этой адаптации заключается в минимизации числа операций путём использования операций с как можно более длинными операндами. Сделать это позволяют такие технологии, как, например, SIMD, SSE2, AVX.

примеры реализации на языке C

Для пояснения работы функций, а также для того, чтобы показать константы раундов, будут приводиться куски кода на C^[3]. Будучи соединёнными в один файл и дополненными функцией main(), приведённой ниже, они компилируются^[4]; полученная программа реализует функцию $E_{8}$ .

предварительные объявления на C

#include <emmintrin.h>
#include <stdlib.h>
#include <stdio.h>

typedef __m128i  word128;   /*word128 defines a 128-bit SSE2 word*/

/*define data alignment for different C compilers*/
#if defined(__GNUC__)
      #define DATA_ALIGN16(x) x __attribute__ ((aligned(16)))
#else
      #define DATA_ALIGN16(x) __declspec(align(16)) x
#endif

/*The following defines operations on 128-bit word(s)*/
#define CONSTANT(b)   _mm_set1_epi8((b))          /*set each byte in a 128-bit register to be "b"*/

#define XOR(x,y)      _mm_xor_si128((x),(y))      /*XOR(x,y) = x ^ y, where x and y are two 128-bit word*/
#define AND(x,y)      _mm_and_si128((x),(y))      /*AND(x,y) = x & y, where x and y are two 128-bit word*/
#define ANDNOT(x,y)   _mm_andnot_si128((x),(y))   /*ANDNOT(x,y) = (!x) & y, where x and y are two 128-bit word*/
#define OR(x,y)       _mm_or_si128((x),(y))       /*OR(x,y)  = x | y, where x and y are two 128-bit word*/

#define SHR1(x)       _mm_srli_epi16((x), 1)      /*SHR1(x)  = x >> 1, where x is a 128 bit word*/
#define SHR2(x)       _mm_srli_epi16((x), 2)      /*SHR2(x)  = x >> 2, where x is a 128 bit word*/
#define SHR4(x)       _mm_srli_epi16((x), 4)      /*SHR4(x)  = x >> 4, where x is a 128 bit word*/
#define SHR8(x)       _mm_slli_epi16((x), 8)      /*SHR8(x)  = x >> 8, where x is a 128 bit word*/
#define SHR16(x)      _mm_slli_epi32((x), 16)     /*SHR16(x) = x >> 16, where x is a 128 bit word*/
#define SHR32(x)      _mm_slli_epi64((x), 32)     /*SHR32(x) = x >> 32, where x is a 128 bit word*/
#define SHR64(x)      _mm_slli_si128((x), 8)      /*SHR64(x) = x >> 64, where x is a 128 bit word*/

#define SHL1(x)       _mm_slli_epi16((x), 1)      /*SHL1(x)  = x << 1, where x is a 128 bit word*/
#define SHL2(x)       _mm_slli_epi16((x), 2)    /*SHL2(x)  = x << 2, where x is a 128 bit word*/
#define SHL4(x)       _mm_slli_epi16((x), 4)    /*SHL4(x)  = x << 4, where x is a 128 bit word*/
#define SHL8(x)       _mm_srli_epi16((x), 8)    /*SHL8(x)  = x << 8, where x is a 128 bit word*/
#define SHL16(x)      _mm_srli_epi32((x), 16)   /*SHL16(x) = x << 16, where x is a 128 bit word*/
#define SHL32(x)      _mm_srli_epi64((x), 32)   /*SHL32(x) = x << 32, where x is a 128 bit word*/
#define SHL64(x)      _mm_srli_si128((x), 8)    /*SHL64(x) = x << 64, where x is a 128 bit word*/

Пример функции main()

int main()
{
	int j;
	void* e8_out;
	
	//here can be any constant you like to use for E8 check
	char e8_in[128]={0,0xe0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
		

	e8_out=(void*)calloc(9,sizeof(word128));

	//16 byte allignment - important!
	e8_out=(void*)(((int) e8_out) + 16 - (((int) e8_out) & 15));
		
	for (j = 0; j < 128; j++)
		*((char*)e8_out+j)=e8_in[j];

	printf("\ninput\n");
	for (j = 0; j < 128; j++)
		printf("%.2x",(char)(*((char*)e8_out+j)) & 0xff);

	E8((word128*)e8_out);

        //out must be equal
        //2dfedd62f99a98acae7cacd619d634e7a4831005bc301216b86038c6c966149466d9899f2580706fce9ea31b1d9b1adc11e8325f7b366e10f994857f02fa06c11b4f1b5cd8c840b397f6a17f6e738099dcdf93a5adeaa3d3a431e8dec9539a6822b4a98aec86a1e4d574ac959ce56cf015960deab5ab2bbf9611dcf0dd64ea6e
	printf("\noutput\n");
	for (j = 0; j < 128; j++)
		printf("%.2x",(char)(*((char*)e8_out+j)) & 0xff);
	
	return(0);
}

Функция SBox

Преобразует четыре 128-битных вектора в зависимости от 128-битной константы. То есть

$(x_{0},x_{1},x_{2},x_{3})=SBox(x_{00},x_{10},x_{20},x_{30},c)$

Алгоритм таков. Введём ещё 128-битную переменную t и проинициализируем переменные начальными значениями

$(x_{0},x_{1},x_{2},x_{3})=(x_{00},x_{10},x_{20},x_{30})$ ,

тогда последовательность присваиваний следующая:

$x_{3}=\neg x_{3}$
$x_{0}=x_{0}\oplus (c~\&~(\neg x_{2}))$
$t~~=c~\oplus (x_{0}~\&~x_{1})$
$x_{0}=x_{0}\oplus (x_{2}~\&~x_{3})$
$x_{3}=x_{3}\oplus ((\neg x_{1})~\&~x_{2})$
$x_{1}=x_{1}\oplus (x_{0}~\&~x_{2})$
$x_{2}=x_{2}\oplus (x_{0}~\&~(\neg x_{3}))$
$x_{0}=x_{0}\oplus (x_{1}|x_{3})$
$x_{3}=x_{3}\oplus (x_{1}~\&~x_{2})$
$x_{1}=x_{1}\oplus (t~\&~x_{0})$
$x_{2}=x_{2}\oplus t$

возможная реализация на C

/*Sbox implements S0 and S1, selected by a constant bit*/
#define S_BOX(m0,m1,m2,m3,cnst)  {    \
      word128 t;                         \
      m3 = XOR(m3,CONSTANT(0xff));       \
      m0 = XOR(m0,ANDNOT(m2,cnst));     \
      t  = XOR(cnst,AND(m0,m1));        \
      m0 = XOR(m0,AND(m3,m2));           \
      m3 = XOR(m3,ANDNOT(m1,m2));        \
      m1 = XOR(m1,AND(m0,m2));           \
      m2 = XOR(m2,ANDNOT(m3,m0));        \
      m0 = XOR(m0,OR(m1,m3));            \
      m3 = XOR(m3,AND(m1,m2));           \
      m2 = XOR(m2,t);                   \
      m1 = XOR(m1,AND(t,m0));           \
     }

- описание используемых макросов см. в блоке "предварительные объявления на C"

Функция LinTrans

Преобразует восемь 128-битных переменных. Пусть $(b_{0},b_{1},b_{2},b_{3},b_{4},b_{5},b_{6},b_{7})=LinTrans(a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7})$ , тогда

$b_{4}=a_{4}\oplus a_{1}$

$b_{5}=a_{5}\oplus a_{2}$

$b_{6}=a_{6}\oplus a_{3}\oplus a_{0}$

$b_{7}=a_{7}\oplus a_{0}$

$b_{0}=a_{0}\oplus b_{5}$

$b_{1}=a_{1}\oplus b_{6}$

$b_{2}=a_{2}\oplus b_{7}\oplus b_{4}$

$b_{3}=a_{3}\oplus b_{4}$

возможная реализация на C

/*The MDS code*/
#define LIN_TRANS(word)     \
      word[1] = XOR(word[1],word[2]);           \
      word[3] = XOR(word[3],word[4]);           \
      word[5] = XOR(XOR(word[5],word[6]),word[0]);   \
      word[7] = XOR(word[7],word[0]);           \
      word[0] = XOR(word[0],word[3]);           \
      word[2] = XOR(word[2],word[5]);           \
      word[4] = XOR(XOR(word[4],word[7]),word[1]);   \
      word[6] = XOR(word[6],word[1]);

В коде для удобства дальнейшего использования $a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7}$ соответствует (word[0],word[2],word[4],word[6],word[1],word[3],word[5],word[7])

- описание используемых макросов см. в блоке "предварительные объявления на C"

Функция Permutation

Преобразует 128-битную переменную в зависимости от целой константы $n:~6\geq n\geq 0$ . Эта функция не оптимизируется для использования 128-битных переменных, однако для совместного использования с другими функциями из этого раздела она необходима.

Пусть $b=Permutation(a,n)$ , $b=b_{0}||b_{1}||\dots ||b_{127},a=a_{0}||a_{1}||\dots ||a_{127}$ где. Алгоритм получения числа $b$ таков:

$b=a$ :

for~i=0~~to~{\frac {128}{2\times 2^{n}}}-1~~begin

Swap{\Big (}(b_{2\times 2^{n}\times i+0}||b_{2\times 2^{n}\times i+1}||\dots ||b_{2\times 2^{n}\times i+2^{n}-1}),~(b_{2\times 2^{n}\times i+2^{n}+0}||b_{2\times 2^{n}\times i+2^{n}+1}||\dots ||b_{2\times 2^{n}\times i+2^{n}+2^{n}-1}){\Big )}

end

Здесь запись $Swap(p,q)$ означает такой участок алгоритма, после которого переменная $p$ принимает значение, которое было у переменной $q$ , а переменная $q$ принимает значение, которое было у переменной $p$ .

возможная реализация на C

/*The following defines operations on 128-bit word(s)*/
#define SWAP0(x)      OR(SHR1(AND((x),CONSTANT(0xaa))),SHL1(AND((x),CONSTANT(0x55))))  /*swapping bit 2i with bit 2i+1 of the 128-bit x */
#define SWAP1(x)      OR(SHR2(AND((x),CONSTANT(0xcc))),SHL2(AND((x),CONSTANT(0x33))))  /*swapping bit 4i||4i+1 with bit 4i+2||4i+3 of the 128-bit x */
#define SWAP2(x)      OR(SHR4(AND((x),CONSTANT(0xf0))),SHL4(AND((x),CONSTANT(0xf))))   /*swapping bits 8i||8i+1||8i+2||8i+3 with bits 8i+4||8i+5||8i+6||8i+7 of the 128-bit x */
#define SWAP3(x)      OR(SHR8(x),SHL8(x))                          /*swapping bits 16i||16i+1||...||16i+7 with bits 16i+8||16i+9||...||16i+15 of the 128-bit x */
#define SWAP4(x)     OR(SHR16(x),SHL16(x))                        /*swapping bits 32i||32i+1||...||32i+15 with bits 32i+16||32i+17||...||32i+31 of the 128-bit x */
#define SWAP5(x)     _mm_shuffle_epi32((x),_MM_SHUFFLE(2,3,0,1))  /*swapping bits 64i||64i+1||...||64i+31 with bits 64i+32||64i+33||...||64i+63 of the 128-bit x*/
#define SWAP6(x)     _mm_shuffle_epi32((x),_MM_SHUFFLE(1,0,3,2))  /*swapping bits 128i||128i+1||...||128i+63 with bits 128i+64||128i+65||...||128i+127 of the 128-bit x*/
#define STORE(x,p)    _mm_store_si128((__m128i *)(p), (x))         /*store the 128-bit word x into memeory address p, where p is the multile of 16 bytes*/
#define LOAD(p)       _mm_load_si128((__m128i *)(p))               /*load 16 bytes from the memory address p, return a 128-bit word, where p is the multile of 16 bytes*/

#define PERMUTATION(word,n)         \
      word[1] = SWAP##n(word[1]); word[3] = SWAP##n(word[3]); word[5] = SWAP##n(word[5]); word[7] = SWAP##n(word[7]);

- описание используемых макросов см. в блоке «предварительные объявления на C»

Функция E₈, адаптированная к программной реализации

Преобразует 1024-битный вектор. Совпадает с функцией $E_{8}$ , описанной в обобщённом случае (в том смысле, что при совпадении значений аргументов совпадают значения функций). Пусть на вход поступил 1024-битный вектор. Представим его в виде набора 8-ми 128-битных переменных: $(x_{0},x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7})$ . После следующих преобразований они будут представлять собой выходной вектор:

for~r=0~~to~41~~begin

(x_{0},x_{2},x_{4},x_{6})=SBox(x_{0},x_{2},x_{4},x_{6},C_{r}^{even})

(x_{1},x_{3},x_{5},x_{7})=SBox(x_{1},x_{3},x_{5},x_{7},C_{r}^{odd})

(x_{0},x_{2},x_{4},x6_{,}x_{1},x_{3},x_{5},x_{7})=LinTrans(x_{0},x_{2},x_{4},x_{6},x_{1},x_{3},x_{5},x_{7})

x_{1}=Permutation(x_{1},r{\bmod {7}})

x_{3}=Permutation(x_{3},r{\bmod {7}})

x_{5}=Permutation(x_{5},r{\bmod {7}})

x_{7}=Permutation(x_{7},r{\bmod {7}})

end

Использующиеся 128-битные константы задаются следующим образом: $C_{r}^{odd}=C_{r}^{1}||C_{r}^{3}||\dots ||C_{r}^{255},~C_{r}^{even}=C_{r}^{0}||C_{r}^{2}||\dots ||C_{r}^{254},~C_{r}=R_{6}(C_{r-1},0),~r=1\dots 42,~C_{0}=\left\lfloor ({\sqrt {2}}-1)\times 2^{256}\right\rfloor$

возможная реализация на C

/*42 round constants, each round constant is 32-byte (256-bit)*/
DATA_ALIGN16(const unsigned char E8_bitslice_roundconstant[42][32])={
{0x72,0xd5,0xde,0xa2,0xdf,0x15,0xf8,0x67,0x7b,0x84,0x15,0xa,0xb7,0x23,0x15,0x57,0x81,0xab,0xd6,0x90,0x4d,0x5a,0x87,0xf6,0x4e,0x9f,0x4f,0xc5,0xc3,0xd1,0x2b,0x40},
{0xea,0x98,0x3a,0xe0,0x5c,0x45,0xfa,0x9c,0x3,0xc5,0xd2,0x99,0x66,0xb2,0x99,0x9a,0x66,0x2,0x96,0xb4,0xf2,0xbb,0x53,0x8a,0xb5,0x56,0x14,0x1a,0x88,0xdb,0xa2,0x31},
{0x3,0xa3,0x5a,0x5c,0x9a,0x19,0xe,0xdb,0x40,0x3f,0xb2,0xa,0x87,0xc1,0x44,0x10,0x1c,0x5,0x19,0x80,0x84,0x9e,0x95,0x1d,0x6f,0x33,0xeb,0xad,0x5e,0xe7,0xcd,0xdc},
{0x10,0xba,0x13,0x92,0x2,0xbf,0x6b,0x41,0xdc,0x78,0x65,0x15,0xf7,0xbb,0x27,0xd0,0xa,0x2c,0x81,0x39,0x37,0xaa,0x78,0x50,0x3f,0x1a,0xbf,0xd2,0x41,0x0,0x91,0xd3},
{0x42,0x2d,0x5a,0xd,0xf6,0xcc,0x7e,0x90,0xdd,0x62,0x9f,0x9c,0x92,0xc0,0x97,0xce,0x18,0x5c,0xa7,0xb,0xc7,0x2b,0x44,0xac,0xd1,0xdf,0x65,0xd6,0x63,0xc6,0xfc,0x23},
{0x97,0x6e,0x6c,0x3,0x9e,0xe0,0xb8,0x1a,0x21,0x5,0x45,0x7e,0x44,0x6c,0xec,0xa8,0xee,0xf1,0x3,0xbb,0x5d,0x8e,0x61,0xfa,0xfd,0x96,0x97,0xb2,0x94,0x83,0x81,0x97},
{0x4a,0x8e,0x85,0x37,0xdb,0x3,0x30,0x2f,0x2a,0x67,0x8d,0x2d,0xfb,0x9f,0x6a,0x95,0x8a,0xfe,0x73,0x81,0xf8,0xb8,0x69,0x6c,0x8a,0xc7,0x72,0x46,0xc0,0x7f,0x42,0x14},
{0xc5,0xf4,0x15,0x8f,0xbd,0xc7,0x5e,0xc4,0x75,0x44,0x6f,0xa7,0x8f,0x11,0xbb,0x80,0x52,0xde,0x75,0xb7,0xae,0xe4,0x88,0xbc,0x82,0xb8,0x0,0x1e,0x98,0xa6,0xa3,0xf4},
{0x8e,0xf4,0x8f,0x33,0xa9,0xa3,0x63,0x15,0xaa,0x5f,0x56,0x24,0xd5,0xb7,0xf9,0x89,0xb6,0xf1,0xed,0x20,0x7c,0x5a,0xe0,0xfd,0x36,0xca,0xe9,0x5a,0x6,0x42,0x2c,0x36},
{0xce,0x29,0x35,0x43,0x4e,0xfe,0x98,0x3d,0x53,0x3a,0xf9,0x74,0x73,0x9a,0x4b,0xa7,0xd0,0xf5,0x1f,0x59,0x6f,0x4e,0x81,0x86,0xe,0x9d,0xad,0x81,0xaf,0xd8,0x5a,0x9f},
{0xa7,0x5,0x6,0x67,0xee,0x34,0x62,0x6a,0x8b,0xb,0x28,0xbe,0x6e,0xb9,0x17,0x27,0x47,0x74,0x7,0x26,0xc6,0x80,0x10,0x3f,0xe0,0xa0,0x7e,0x6f,0xc6,0x7e,0x48,0x7b},
{0xd,0x55,0xa,0xa5,0x4a,0xf8,0xa4,0xc0,0x91,0xe3,0xe7,0x9f,0x97,0x8e,0xf1,0x9e,0x86,0x76,0x72,0x81,0x50,0x60,0x8d,0xd4,0x7e,0x9e,0x5a,0x41,0xf3,0xe5,0xb0,0x62},
{0xfc,0x9f,0x1f,0xec,0x40,0x54,0x20,0x7a,0xe3,0xe4,0x1a,0x0,0xce,0xf4,0xc9,0x84,0x4f,0xd7,0x94,0xf5,0x9d,0xfa,0x95,0xd8,0x55,0x2e,0x7e,0x11,0x24,0xc3,0x54,0xa5},
{0x5b,0xdf,0x72,0x28,0xbd,0xfe,0x6e,0x28,0x78,0xf5,0x7f,0xe2,0xf,0xa5,0xc4,0xb2,0x5,0x89,0x7c,0xef,0xee,0x49,0xd3,0x2e,0x44,0x7e,0x93,0x85,0xeb,0x28,0x59,0x7f},
{0x70,0x5f,0x69,0x37,0xb3,0x24,0x31,0x4a,0x5e,0x86,0x28,0xf1,0x1d,0xd6,0xe4,0x65,0xc7,0x1b,0x77,0x4,0x51,0xb9,0x20,0xe7,0x74,0xfe,0x43,0xe8,0x23,0xd4,0x87,0x8a},
{0x7d,0x29,0xe8,0xa3,0x92,0x76,0x94,0xf2,0xdd,0xcb,0x7a,0x9,0x9b,0x30,0xd9,0xc1,0x1d,0x1b,0x30,0xfb,0x5b,0xdc,0x1b,0xe0,0xda,0x24,0x49,0x4f,0xf2,0x9c,0x82,0xbf},
{0xa4,0xe7,0xba,0x31,0xb4,0x70,0xbf,0xff,0xd,0x32,0x44,0x5,0xde,0xf8,0xbc,0x48,0x3b,0xae,0xfc,0x32,0x53,0xbb,0xd3,0x39,0x45,0x9f,0xc3,0xc1,0xe0,0x29,0x8b,0xa0},
{0xe5,0xc9,0x5,0xfd,0xf7,0xae,0x9,0xf,0x94,0x70,0x34,0x12,0x42,0x90,0xf1,0x34,0xa2,0x71,0xb7,0x1,0xe3,0x44,0xed,0x95,0xe9,0x3b,0x8e,0x36,0x4f,0x2f,0x98,0x4a},
{0x88,0x40,0x1d,0x63,0xa0,0x6c,0xf6,0x15,0x47,0xc1,0x44,0x4b,0x87,0x52,0xaf,0xff,0x7e,0xbb,0x4a,0xf1,0xe2,0xa,0xc6,0x30,0x46,0x70,0xb6,0xc5,0xcc,0x6e,0x8c,0xe6},
{0xa4,0xd5,0xa4,0x56,0xbd,0x4f,0xca,0x0,0xda,0x9d,0x84,0x4b,0xc8,0x3e,0x18,0xae,0x73,0x57,0xce,0x45,0x30,0x64,0xd1,0xad,0xe8,0xa6,0xce,0x68,0x14,0x5c,0x25,0x67},
{0xa3,0xda,0x8c,0xf2,0xcb,0xe,0xe1,0x16,0x33,0xe9,0x6,0x58,0x9a,0x94,0x99,0x9a,0x1f,0x60,0xb2,0x20,0xc2,0x6f,0x84,0x7b,0xd1,0xce,0xac,0x7f,0xa0,0xd1,0x85,0x18},
{0x32,0x59,0x5b,0xa1,0x8d,0xdd,0x19,0xd3,0x50,0x9a,0x1c,0xc0,0xaa,0xa5,0xb4,0x46,0x9f,0x3d,0x63,0x67,0xe4,0x4,0x6b,0xba,0xf6,0xca,0x19,0xab,0xb,0x56,0xee,0x7e},
{0x1f,0xb1,0x79,0xea,0xa9,0x28,0x21,0x74,0xe9,0xbd,0xf7,0x35,0x3b,0x36,0x51,0xee,0x1d,0x57,0xac,0x5a,0x75,0x50,0xd3,0x76,0x3a,0x46,0xc2,0xfe,0xa3,0x7d,0x70,0x1},
{0xf7,0x35,0xc1,0xaf,0x98,0xa4,0xd8,0x42,0x78,0xed,0xec,0x20,0x9e,0x6b,0x67,0x79,0x41,0x83,0x63,0x15,0xea,0x3a,0xdb,0xa8,0xfa,0xc3,0x3b,0x4d,0x32,0x83,0x2c,0x83},
{0xa7,0x40,0x3b,0x1f,0x1c,0x27,0x47,0xf3,0x59,0x40,0xf0,0x34,0xb7,0x2d,0x76,0x9a,0xe7,0x3e,0x4e,0x6c,0xd2,0x21,0x4f,0xfd,0xb8,0xfd,0x8d,0x39,0xdc,0x57,0x59,0xef},
{0x8d,0x9b,0xc,0x49,0x2b,0x49,0xeb,0xda,0x5b,0xa2,0xd7,0x49,0x68,0xf3,0x70,0xd,0x7d,0x3b,0xae,0xd0,0x7a,0x8d,0x55,0x84,0xf5,0xa5,0xe9,0xf0,0xe4,0xf8,0x8e,0x65},
{0xa0,0xb8,0xa2,0xf4,0x36,0x10,0x3b,0x53,0xc,0xa8,0x7,0x9e,0x75,0x3e,0xec,0x5a,0x91,0x68,0x94,0x92,0x56,0xe8,0x88,0x4f,0x5b,0xb0,0x5c,0x55,0xf8,0xba,0xbc,0x4c},
{0xe3,0xbb,0x3b,0x99,0xf3,0x87,0x94,0x7b,0x75,0xda,0xf4,0xd6,0x72,0x6b,0x1c,0x5d,0x64,0xae,0xac,0x28,0xdc,0x34,0xb3,0x6d,0x6c,0x34,0xa5,0x50,0xb8,0x28,0xdb,0x71},
{0xf8,0x61,0xe2,0xf2,0x10,0x8d,0x51,0x2a,0xe3,0xdb,0x64,0x33,0x59,0xdd,0x75,0xfc,0x1c,0xac,0xbc,0xf1,0x43,0xce,0x3f,0xa2,0x67,0xbb,0xd1,0x3c,0x2,0xe8,0x43,0xb0},
{0x33,0xa,0x5b,0xca,0x88,0x29,0xa1,0x75,0x7f,0x34,0x19,0x4d,0xb4,0x16,0x53,0x5c,0x92,0x3b,0x94,0xc3,0xe,0x79,0x4d,0x1e,0x79,0x74,0x75,0xd7,0xb6,0xee,0xaf,0x3f},
{0xea,0xa8,0xd4,0xf7,0xbe,0x1a,0x39,0x21,0x5c,0xf4,0x7e,0x9,0x4c,0x23,0x27,0x51,0x26,0xa3,0x24,0x53,0xba,0x32,0x3c,0xd2,0x44,0xa3,0x17,0x4a,0x6d,0xa6,0xd5,0xad},
{0xb5,0x1d,0x3e,0xa6,0xaf,0xf2,0xc9,0x8,0x83,0x59,0x3d,0x98,0x91,0x6b,0x3c,0x56,0x4c,0xf8,0x7c,0xa1,0x72,0x86,0x60,0x4d,0x46,0xe2,0x3e,0xcc,0x8,0x6e,0xc7,0xf6},
{0x2f,0x98,0x33,0xb3,0xb1,0xbc,0x76,0x5e,0x2b,0xd6,0x66,0xa5,0xef,0xc4,0xe6,0x2a,0x6,0xf4,0xb6,0xe8,0xbe,0xc1,0xd4,0x36,0x74,0xee,0x82,0x15,0xbc,0xef,0x21,0x63},
{0xfd,0xc1,0x4e,0xd,0xf4,0x53,0xc9,0x69,0xa7,0x7d,0x5a,0xc4,0x6,0x58,0x58,0x26,0x7e,0xc1,0x14,0x16,0x6,0xe0,0xfa,0x16,0x7e,0x90,0xaf,0x3d,0x28,0x63,0x9d,0x3f},
{0xd2,0xc9,0xf2,0xe3,0x0,0x9b,0xd2,0xc,0x5f,0xaa,0xce,0x30,0xb7,0xd4,0xc,0x30,0x74,0x2a,0x51,0x16,0xf2,0xe0,0x32,0x98,0xd,0xeb,0x30,0xd8,0xe3,0xce,0xf8,0x9a},
{0x4b,0xc5,0x9e,0x7b,0xb5,0xf1,0x79,0x92,0xff,0x51,0xe6,0x6e,0x4,0x86,0x68,0xd3,0x9b,0x23,0x4d,0x57,0xe6,0x96,0x67,0x31,0xcc,0xe6,0xa6,0xf3,0x17,0xa,0x75,0x5},
{0xb1,0x76,0x81,0xd9,0x13,0x32,0x6c,0xce,0x3c,0x17,0x52,0x84,0xf8,0x5,0xa2,0x62,0xf4,0x2b,0xcb,0xb3,0x78,0x47,0x15,0x47,0xff,0x46,0x54,0x82,0x23,0x93,0x6a,0x48},
{0x38,0xdf,0x58,0x7,0x4e,0x5e,0x65,0x65,0xf2,0xfc,0x7c,0x89,0xfc,0x86,0x50,0x8e,0x31,0x70,0x2e,0x44,0xd0,0xb,0xca,0x86,0xf0,0x40,0x9,0xa2,0x30,0x78,0x47,0x4e},
{0x65,0xa0,0xee,0x39,0xd1,0xf7,0x38,0x83,0xf7,0x5e,0xe9,0x37,0xe4,0x2c,0x3a,0xbd,0x21,0x97,0xb2,0x26,0x1,0x13,0xf8,0x6f,0xa3,0x44,0xed,0xd1,0xef,0x9f,0xde,0xe7},
{0x8b,0xa0,0xdf,0x15,0x76,0x25,0x92,0xd9,0x3c,0x85,0xf7,0xf6,0x12,0xdc,0x42,0xbe,0xd8,0xa7,0xec,0x7c,0xab,0x27,0xb0,0x7e,0x53,0x8d,0x7d,0xda,0xaa,0x3e,0xa8,0xde},
{0xaa,0x25,0xce,0x93,0xbd,0x2,0x69,0xd8,0x5a,0xf6,0x43,0xfd,0x1a,0x73,0x8,0xf9,0xc0,0x5f,0xef,0xda,0x17,0x4a,0x19,0xa5,0x97,0x4d,0x66,0x33,0x4c,0xfd,0x21,0x6a},
{0x35,0xb4,0x98,0x31,0xdb,0x41,0x15,0x70,0xea,0x1e,0xf,0xbb,0xed,0xcd,0x54,0x9b,0x9a,0xd0,0x63,0xa1,0x51,0x97,0x40,0x72,0xf6,0x75,0x9d,0xbf,0x91,0x47,0x6f,0xe2}};

/*the round function of E8 */
#define ROUND_FUNCTION(word,n,r)\
	S_BOX(((word)[0]),((word)[2]),((word)[4]),((word)[6]),(LOAD(E8_bitslice_roundconstant[r]))) \
	S_BOX(((word)[1]),((word)[3]),((word)[5]),((word)[7]),(LOAD(E8_bitslice_roundconstant[r]+16))) \
	LIN_TRANS(word) \
	PERMUTATION((word),n)

void E8(word128 *word){
    int i;
    for (i = 0; i < 42; i = i+7) {
        ROUND_FUNCTION(word,0,i)
        ROUND_FUNCTION(word,1,i+1)
        ROUND_FUNCTION(word,2,i+2)
        ROUND_FUNCTION(word,3,i+3)
        ROUND_FUNCTION(word,4,i+4)
        ROUND_FUNCTION(word,5,i+5)
        ROUND_FUNCTION(word,6,i+6)
    }
}

- описание используемых макросов см. в подразделах выше.

Исходные данные

Входной параметр

$l_{hash}$ — длина хэша (число бит в выходном векторе хеш-функции).

Может принимать только следующие значения:

224, 256, 384 и 512;

напомним, что данная статья, строго говоря, описывает семейство из 4-х хеш-функций.

Входное сообщение

Представляет собой число — длину сообщения $L$ и битовый вектор $M_{0}$ (если $L\neq 0$ ). Даже если $L=0$ никаких трудностей для вычисления $JH(M_{0})$ не возникает.

Алгоритм вычисления JH(M₀)

1) Дополнение входного вектора

Присоединение к сообщению

M_{0}

дополнительных бит в конце. Происходит в три этапа:

1.1)Дополнение единицей.

Присоединение к концу сообщения единичного бита.

1.2)Дополнение нулями.

Присоединение к концу сообщения, дополненного единицей, нулевых бит в количестве

383+(-L{\bmod {5}}12)

штук.

1.3)Дополнение длиной сообщения.

Присоединение к концу сообщения, дополненного единицей и нулями, 128 бит, в которых записана длина исходного сообщения (например, если

L=2

, то добавка будет выглядеть так:

0\dots 010

).

В итоге получится дополненное сообщение

M

с длиной, кратной

512

.

2) Свёртка дополненного входного вектора функцией $F_{8}$

M

разбивается на блоки по

512

бит. Обозначим за

N

число таких блоков.

Свёртка происходит за

N

итераций. На

i

-той итерации на вход

F_{8}

поступает

i

-й

512

-битный блок

M_{i}

сообщения

M

и значение

H_{i-1}=F_{8}(H_{i-2},M_{i-1})

, вычисленное на предыдущей итерации. Имеется также нулевая итерация, на которой вычисляется

H_{0}

из

H_{-1}

и

M_{0}

. Таким образом имеем:

H=H_{N}=F_{8}(H_{N-1},M_{N})=F_{8}(F_{8}(H_{N-2},M_{N-1}),M_{N})=\dots =F_{8}(\dots (H_{-1},M_{0})\dots )

.

H_{-1}

и

M_{0}

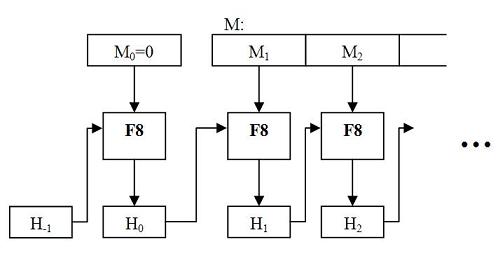
выбираются так: первые

16

бит

H_{-1}

равны входному параметру

l_{hash}

— размеру выходного хэша (для

l_{hash}

, равных

512,~324,~256

или

224

это соответственно 0200h, 0180h, 0100h или 00e0h), а остальные биты

H_{-1}

и все биты

M_{0}

задаются равными

0

.

3) Выборка хэша из выхода функции $F_{8}$

Из

1024

-битного вектора

H_{N}=H_{N}^{0}||H_{N}^{1}||\dots ||H_{N}^{1023}

, полученного на выходе

F_{8}

на последней итерации свёртки дополненного входного сообщения, выбираются последние

l_{hash}

бит:

JH(M_{0})=H_{N}^{1023+1-l_{hash}}||H_{N}^{1023+2-l_{hash}}||\dots ||H_{N}^{1023}

Криптоанализ

См. также

Примечания

↑ сравнение финалистов второго тура SHA по параметрам реализации на различных ПЛИС http://www.ecrypt.eu.org/hash2011/proceedings/hash2011_07.pdf Архивная копия от 23 августа 2011 на Wayback Machine
↑ алгоритм взят здесь: http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_round3.pdf Архивная копия от 10 ноября 2011 на Wayback Machine
↑ Эти куски взяты по адресу http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_sse2_opt64.h Архивная копия от 4 декабря 2011 на Wayback Machine и изменены для ясности и простоты.
↑ При использовании компилятора gcc для того, чтобы он подразумевал возможность использования дополнительных командных наборов, поддерживаемых процессором, типа SSE2, в командную строку при компиляции можно добавить опцию -march=native (например "gcc -o prog prog.c -Wall -march=native").

Ссылки

документация, актуальная в ноябре 2011 года
- http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_round3.pdf Архивная копия от 10 ноября 2011 на Wayback Machine
варианты исходных кодов на VHDL моделей электронных устройств, реализующих JH:
варианты исходных кодов на C, реализующих JH:
- http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_ref.h Архивная копия от 4 ноября 2011 на Wayback Machine
- http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_bitslice_ref64.h Архивная копия от 11 августа 2011 на Wayback Machine
- http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_sse2_opt64.h Архивная копия от 4 декабря 2011 на Wayback Machine
страница автора для поддержки JH
- http://www3.ntu.edu.sg/home/wuhj/research/jh/index.html Архивная копия от 4 декабря 2011 на Wayback Machine
ссылки на исследования криптоаналитиков и архивы файлов, отправлявшиеся на конкурс SHA-3
- http://ehash.iaik.tugraz.at/wiki/JH
ссылки на архивы с исходными кодами на VHDL (и сопутствующими файлами) моделей электронных устройств, реализующих алгоритмы хеш-функций, прошедших во второй тур SHA-3
- http://cryptography.gmu.edu/athena/index.php?id=source_codes
ссылки на исследования характеристик электронных устройств (реализованных на ПЛИС), реализующих алгоритмы хеш-функций, прошедших в финал второго тура SHA-3
- http://ehash.iaik.tugraz.at/wiki/SHA-3_Hardware_Implementations
- https://web.archive.org/web/20120628192806/http://rijndael.ece.vt.edu/sha3/publications.html

[1] сравнение финалистов второго тура SHA по параметрам реализации на различных ПЛИС http://www.ecrypt.eu.org/hash2011/proceedings/hash2011_07.pdf Архивная копия от 23 августа 2011 на Wayback Machine

[2] алгоритм взят здесь: http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_round3.pdf Архивная копия от 10 ноября 2011 на Wayback Machine

[3] Эти куски взяты по адресу http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_sse2_opt64.h Архивная копия от 4 декабря 2011 на Wayback Machine и изменены для ясности и простоты.

[4] При использовании компилятора gcc для того, чтобы он подразумевал возможность использования дополнительных командных наборов, поддерживаемых процессором, типа SSE2, в командную строку при компиляции можно добавить опцию -march=native (например "gcc -o prog prog.c -Wall -march=native").

[1]

[2]

[3]

[4]

Хеш-функции
Общего назначения	Adler-32 CRC Контрольная сумма Флетчера FNV MurmurHash2 MurmurHash2A MurmurHash3 PJW-32 TTH-Дерево хешей Jenkins hash Хеш-сумма
Криптографические	ГОСТ Р 34.11-94 Стрибог BelT BLAKE Blue Midnight Wish CubeHash ECHO Edonkey2k FSB Fugue Grøstl HAVAL Hamsi JH Kupyna LM-хеш Luffa MASH-1 MD2 MD4 MD5 MD6 N-Hash RIPEMD-128 RIPEMD-160 RIPEMD-256 RIPEMD-320 SHA-1 SHA-2 SHA-3 (Keccak) SHABAL SHAvite-3 SIMD SWIFFT Skein Snefru Tiger Whirlpool
Функции формирования ключа	bcrypt PBKDF2 scrypt Argon2 Lyra2
Контрольное число (сравнение)	Контрольная сумма Алгоритм Верхуффа Алгоритм Дамма Алгоритм Луна Штрих-код Банковских счетов Банковских карт ISIN СНИЛС ОКПО ИНН ОКАТО ISBN ОГРН и ОГРНИП VIN
Применение хешей	Сравнение контрольных чисел Коллизия хеш-функции Протоколы аутентификации Сравнение штрихкодов Криптография Magnet-ссылка Подпись Меркла ed2k URN

JH

Содержание

Алгоритм^[2]

Уточнения

О названии элементов битовых векторов

Обозначение конкатенации

Используемые функции — обобщённый случай

S-box — S_i(x)

Линейное преобразование пар ячеек — L(A,B)

Перемешивание — P_d

Преобразование-раунд — R_d(A,C)

Преобразование E_d

Функция свёртки F_d(H,M)

Используемые функции — адаптация к аппаратной реализации при d=8

Выражение преобразования L через простые операции с битами

Константы H₀ при разных l_hash

Константы C раундов R₈

Позиции полубайтов после перемешивания P₈

Используемые функции — адаптация к программной реализации при d=8

примеры реализации на языке C

Функция SBox

Функция LinTrans

Функция Permutation

Функция E₈, адаптированная к программной реализации

Исходные данные

Входной параметр

Входное сообщение

Алгоритм вычисления JH(M₀)

Криптоанализ

См. также

Примечания

Ссылки

Похожие исследовательские статьи

JH

Алгоритм[2]

Уточнения

О названии элементов битовых векторов

Обозначение конкатенации

Используемые функции — обобщённый случай

S-box — .mw-parser-output .ts-math{white-space:nowrap;font-family:times,serif,palatino linotype,new athena unicode,athena,gentium,code2000;font-size:120%}Si(x)

Линейное преобразование пар ячеек — L(A,B)

Перемешивание — Pd

Преобразование-раунд — Rd(A,C)

Преобразование Ed

Функция свёртки Fd(H,M)

Используемые функции — адаптация к аппаратной реализации при d=8

Выражение преобразования L через простые операции с битами

Константы H0 при разных lhash

Константы C раундов R8

Позиции полубайтов после перемешивания P8

Используемые функции — адаптация к программной реализации при d=8

примеры реализации на языке C

Функция SBox

Функция LinTrans

Функция Permutation

Функция E8, адаптированная к программной реализации

Исходные данные

Входной параметр

Входное сообщение

Алгоритм вычисления JH(M0)

Криптоанализ

См. также

Примечания

Ссылки

Похожие исследовательские статьи

Алгоритм^[2]

S-box — S_i(x)

Перемешивание — P_d

Преобразование-раунд — R_d(A,C)

Преобразование E_d

Функция свёртки F_d(H,M)

Константы H₀ при разных l_hash

Константы C раундов R₈

Позиции полубайтов после перемешивания P₈

Функция E₈, адаптированная к программной реализации

Алгоритм вычисления JH(M₀)