KHAZAD
| KHAZAD | |
|---|---|
 | |
| Создатель | Винсент Рэймен и Пауло Баррето |
| Создан | 2000 г. |
| Опубликован | 2000 г. |
| Размер ключа | 128 бит |
| Размер блока | 64 бит |
| Число раундов | 8 |
| Тип | Подстановочно-перестановочная сеть |
KHAZAD — в криптографии симметричный блочный шифр, разработанный двумя криптографами: бельгийцем Винсентом Рэйменом (автор шифра Rijndael) и бразильцем Пауло Баррето[англ.]. В алгоритме используются блоки данных размером 64 бита (8 байт) и ключи размером 128 бит. KHAZAD был представлен на европейском конкурсе криптографических примитивов NESSIE в 2000 году, где в модифицированной (tweaked) форме стал одним из алгоритмов-финалистов (но не победителем).[1]
Предшественником алгоритма KHAZAD считается разработанный в 1995 г. Винсентом Рэйменом и Йоаном Дайменом шифр SHARK. Авторы KHAZAD утверждают, что в основе алгоритма лежит стратегия разработки криптографически стойких алгоритмов шифрования (Wide-Trail strategy), предложенная Йоаном Дайменом.[2]
Алгоритм KHAZAD имеет консервативные параметры и создан для замены существующих шифров с 64 битным блоком, таких как IDEA и DES, обеспечивая более высокий уровень безопасности при высокой скорости выполнения.[]
В шифре широко используют инволюционные преобразования, что минимизирует разницу между алгоритмами шифрования и расшифрования.
Описание шифра
KHAZAD — итеративный блочный шифр с размером блока 64 бита и 128-битным ключом. Входной блок данных представляется в виде строки из 8 байт.
S-блок и матрица перемешивания выбраны таким образом, который гарантирует, что шифрование и расшифрование — одна и та же операция (инволюция), за исключением раундовых подключей.
KHAZAD, как и алгоритм AES (Rijndael), принадлежит к семейству блочных шифров, произошедших от шифра SHARK.[3][4]

Основные отличия от SHARK представлены в таблице[1]:
| SHARK | KHAZAD | |
|---|---|---|
| Количество раундов | 6 | 8 |
| Расписание (расширение) ключа | Аффинное преобразование, полученное в результате работы шифра в режиме обратной связи по шифрованному тексту | Схема Фейстеля, где функцией Фейстеля является раундовая функция шифра |
| Неприводимый многочлен поля | (0x1F5) | (0x11D) |
| Реализация S-блока | Отображение в поле + аффинное преобразование | Рекурсивная структура P- и Q-миниблоков |
| Реализация матрицы перемешивания | Код Рида-Соломона | Инволюционный MDS-код |
Первоначальный вариант шифра KHAZAD (названный KHAZAD-0) сейчас является устаревшим. Текущий (финальный) вид шифра был модифицирован («tweaked»), чтобы адаптировать его под аппаратную реализацию. В этой форме KHAZAD и был признан финалистом NESSIE. Модификация не затронула базовую структуру шифра. В нём S-блок, который первоначально генерировался полностью случайно (без чёткого определения какой-либо внутренней структуры), заменен на рекурсивную структуру: новый блок замены 8x8 составлен из маленьких псевдослучайно генерируемых 4x4 мини-блоков (P- и Q-блоки).[1]
Структура алгоритма
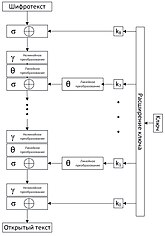

Применением к ключу процедуры расширения ключа получают набор раундовых ключей .
Алгоритм включает 8 раундов, каждый из которых состоит из 3 этапов:
- нелинейное преобразование
- линейное преобразование
- добавление раундового ключа
Перед первым раундом выполняется отбеливание — . Операция не выполняется в последнем раунде.
В операторном виде алгоритм записывается следующим образом:
Шифрование:
Расшифрование:
Набор раундовых ключей получают путём применения к ключу шифрования процедуры расширения ключа.
Структура раунда
Раундовое преобразование можно записать так: .
Нелинейное преобразование
В каждом раунде входной блок разбивается на 8 байт, которые независимо подвергаются нелинейному преобразованию (замене), то есть параллельно проходят через одинаковые S-блоки (каждый S-блок — 8x8 бит, то есть 8 бит на входе и 8 бит на выходе). Блоки замены в оригинальном и модифицированном (tweaked) шифре различаются. Блок замены подобран таким образом, чтобы нелинейное преобразование было инволюционным, то есть или .
Линейное преобразование
8-байтная строка данных умножается побайтно на фиксированную матрицу размера 8 х 8, причём умножение байт производится в поле Галуа с неприводимым полиномом (0x11D).
| 1 | 3 | 4 | 5 | 6 | 8 | B | 7 |
| 3 | 1 | 5 | 4 | 8 | 6 | 7 | B |
| 4 | 5 | 1 | 3 | B | 7 | 6 | 8 |
| 5 | 4 | 3 | 1 | 7 | B | 8 | 6 |
| 6 | 8 | B | 7 | 1 | 3 | 4 | 5 |
| 8 | 6 | 7 | B | 3 | 1 | 5 | 4 |
| B | 7 | 6 | 8 | 4 | 5 | 1 | 3 |
| 7 | B | 8 | 6 | 5 | 4 | 3 | 1 |
В вышеупомянутом поле Галуа матрица является симметричной (, ) и ортогональной (). То есть и преобразование, задаваемое этой матрицей является инволюцией: , где — единичная матрица
Наложение раундового ключа
Над 64-битным блоком данных и 64-битным раундовым ключом выполняется побитовая операция XOR.
Расширение ключа

128-битный (16-байтный) ключ разбивается на 2 равные части:
- — старшие 8 байт (с 15-го по 8-й)
- — младшие 8 байт (с 7-го по 0-й)
Ключи вычисляются по схеме Фейстеля:
Здесь:
— функция раунда алгоритма с входным блоком и ключом .
— 64-битная константа, -й байт которой .
Структура нелинейного преобразования и модификация шифра
Оригинальный шифр
В первоначальном варианте шифра (KHAZAD-0) табличная замена представлялась классическим S-блоком и описывалась следующей матрицей:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| 0 | A7 | D3 | E6 | 71 | D0 | AC | 4D | 79 | 3A | C9 | 91 | FC | 1E | 47 | 54 | BD |
| 1 | 8C | A5 | 7A | FB | 63 | B8 | DD | D4 | E5 | B3 | C5 | BE | A9 | 88 | 0C | A2 |
| 2 | 39 | DF | 29 | DA | 2B | A8 | CB | 4C | 4B | 22 | AA | 24 | 41 | 70 | A6 | F9 |
| 3 | 5A | E2 | B0 | 36 | 7D | E4 | 33 | FF | 60 | 20 | 08 | 8B | 5E | AB | 7F | 78 |
| 4 | 7C | 2C | 57 | D2 | DC | 6D | 7E | 0D | 53 | 94 | C3 | 28 | 27 | 06 | 5F | AD |
| 5 | 67 | 5C | 55 | 48 | 0E | 52 | EA | 42 | 5B | 5D | 30 | 58 | 51 | 59 | 3C | 4E |
| 6 | 38 | 8A | 72 | 14 | E7 | C6 | DE | 50 | 8E | 92 | D1 | 77 | 93 | 45 | 9A | CE |
| 7 | 2D | 03 | 62 | B6 | B9 | BF | 96 | 6B | 3F | 07 | 12 | AE | 40 | 34 | 46 | 3E |
| 8 | DB | CF | EC | CC | C1 | A1 | C0 | D6 | 1D | F4 | 61 | 3B | 10 | D8 | 68 | A0 |
| 9 | B1 | 0A | 69 | 6C | 49 | FA | 76 | C4 | 9E | 9B | 6E | 99 | C2 | B7 | 98 | BC |
| A | 8F | 85 | 1F | B4 | F8 | 11 | 2E | 00 | 25 | 1C | 2A | 3D | 05 | 4F | 7B | B2 |
| B | 32 | 90 | AF | 19 | A3 | F7 | 73 | 9D | 15 | 74 | EE | CA | 9F | 0F | 1B | 75 |
| C | 86 | 84 | 9C | 4A | 97 | 1A | 65 | F6 | ED | 09 | BB | 26 | 83 | EB | 6F | 81 |
| D | 04 | 6A | 43 | 01 | 17 | E1 | 87 | F5 | 8D | E3 | 23 | 80 | 44 | 16 | 66 | 21 |
| E | FE | D5 | 31 | D9 | 35 | 18 | 02 | 64 | F2 | F1 | 56 | CD | 82 | C8 | BA | F0 |
| F | EF | E9 | E8 | FD | 89 | D7 | C7 | B5 | A4 | 2F | 95 | 13 | 0B | F3 | E0 | 37 |
Данная таблица полностью эквивалентна используемой в алгоритме Anubis (ещё один алгоритм, разработанный и представленный на конкурс NESSIE теми же авторами).[2]
Принцип выбора S-блока[5]
Любая булева функция может быть представлена в виде полинома Жегалкина (алгебраическая нормальная форма). Нелинейным порядком функции называется порядок полинома Жегалкина, то есть максимальный из порядков его членов.
Если , введем функцию ,
Блок замены — это отображение . Также, на него можно смотреть как на отображение .
, где
Нелинейный порядок S-блока — — минимальный нелинейный порядок среди всех линейных комбинаций компонентов :
-параметр S-блока: , значение называется дифференциальной равномерностью
Корреляция двух булевых функций
-параметр S-блока:
В шифре KHAZAD-0 используется псевдорандомно сгенерированный S-блок, удовлетворяющий следующим требованиям:
- должен быть инволюцией
- -параметр не должен превышать значение
- -параметр не должен превышать значение
- нелинейный порядок должен быть максимальным, а именно, равным 7
Модифицированный шифр
Пользуясь возможностью незначительного изменения алгоритма в течение первого раунда конкурса, авторы Khazad также внесли изменения в свой алгоритм. В новом варианте спецификации алгоритма исходный алгоритм Khazad назван Khazad-0, а название Khazad присвоено модифицированному алгоритму.[2] (Панасенко С. П. «Алгоритмы шифрования. Специальный справочник»)
В модифицированной версии шифра S-блок 8x8 изменён и представлен рекурсивной структурой, состоящей из мини-блоков P и Q, каждый из которых является маленьким блоком замены с 4 битами на входе и выходе (4x4).
Рекурсивная структура блока замены в модифицированном шифре KHAZAD:[6]

| u | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| P(u) | 3 | F | E | 0 | 5 | 4 | B | C | D | A | 9 | 6 | 7 | 8 | 2 | 1 |
| u | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Q(u) | 9 | E | 5 | 6 | A | 2 | 3 | C | F | 0 | 4 | D | 7 | B | 1 | 8 |
Данная структура P- и Q-миниблоков эквивалентна S-блоку со следующей таблицей замены:[1]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| 0 | BA | 54 | 2F | 74 | 53 | D3 | D2 | 4D | 50 | AC | 8D | BF | 70 | 52 | 9A | 4C |
| 1 | EA | D5 | 97 | D1 | 33 | 51 | 5B | A6 | DE | 48 | A8 | 99 | DB | 32 | B7 | FC |
| 2 | E3 | 9E | 91 | 9B | E2 | BB | 41 | 6E | A5 | CB | 6B | 95 | A1 | F3 | B1 | 02 |
| 3 | CC | C4 | 1D | 14 | C3 | 63 | DA | 5D | 5F | DC | 7D | CD | 7F | 5A | 6C | 5C |
| 4 | F7 | 26 | FF | ED | E8 | 9D | 6F | 8E | 19 | A0 | F0 | 89 | 0F | 07 | AF | FB |
| 5 | 08 | 15 | 0D | 04 | 01 | 64 | DF | 76 | 79 | DD | 3D | 16 | 3F | 37 | 6D | 38 |
| 6 | B9 | 73 | E9 | 35 | 55 | 71 | 7B | 8C | 72 | 88 | F6 | 2A | 3E | 5E | 27 | 46 |
| 7 | 0C | 65 | 68 | 61 | 03 | C1 | 57 | D6 | D9 | 58 | D8 | 66 | D7 | 3A | C8 | 3C |
| 8 | FA | 96 | A7 | 98 | EC | B8 | C7 | AE | 69 | 4B | AB | A9 | 67 | 0A | 47 | F2 |
| 9 | B5 | 22 | E5 | EE | BE | 2B | 81 | 12 | 83 | 1B | 0E | 23 | F5 | 45 | 21 | CE |
| A | 49 | 2C | F9 | E6 | B6 | 28 | 17 | 82 | 1A | 8B | FE | 8A | 09 | C9 | 87 | 4E |
| B | E1 | 2E | E4 | E0 | EB | 90 | A4 | 1E | 85 | 60 | 00 | 25 | F4 | F1 | 94 | 0B |
| C | E7 | 75 | EF | 34 | 31 | D4 | D0 | 86 | 7E | AD | FD | 29 | 30 | 3B | 9F | F8 |
| D | C6 | 13 | 06 | 05 | C5 | 11 | 77 | 7C | 7A | 78 | 36 | 1C | 39 | 59 | 18 | 56 |
| E | B3 | B0 | 24 | 20 | B2 | 92 | A3 | C0 | 44 | 62 | 10 | B4 | 84 | 43 | 93 | C2 |
| F | 4A | BD | 8F | 2D | BC | 9C | 6A | 40 | CF | A2 | 80 | 4F | 1F | CA | AA | 42 |
Из таблиц легко заметить, что как в первоначальном варианте, так и в модифицированном S-блоки являются инволюционными, то есть .
Безопасность
Предполагается, что KHAZAD является криптостойким настолько, насколько криптостойким может быть блочный шифр с данными длинами блока и ключа.
Это подразумевает, помимо прочего, следующее:
- наиболее эффективной атакой на нахождение ключа для шифра KHAZAD является полный перебор.
- получение из данных пар открытый текст — шифротекст, информации о других таких парах не может быть осуществлено более эффективно, чем нахождение ключа методом полного перебора.
- ожидаемая сложность поиска ключа методом полного перебора зависит от битовой длины ключа и равна применительно к шифру KHAZAD.
Такой большой запас надежности закладывался в шифр с учётом всех известных атак.[1]
Существуют атаки лишь на усеченный вариант шифра с 5 раундами (Frédéric Muller, 2003).[7]
Как видно, никаких сколько-нибудь серьезных проблем с криптостойкостью алгоритма Khazad обнаружено не было, что отмечено и экспертами конкурса NESSIE. Кроме того, экспертами отмечена весьма высокая скорость шифрования данного алгоритма. Khazad был признан перспективным алгоритмом, весьма интересным для дальнейшего изучения, но не стал одним из победителей конкурса из-за подозрений экспертов, что структура алгоритма может содержать скрытые уязвимости, которые могут быть обнаружены в будущем.
— Панасенко С. П. "Алгоритмы шифрования. Специальный справочник"[2]
Доступность
Шифр KHAZAD не был (и никогда не будет) запатентован. Он может использоваться бесплатно для любых целей.[1]
Оригинальный текст (англ.)KHAZAD is not (and will never be) patented. It may be used free of charge for any purpose.[1]
Название
Шифр назван в честь Кхазад-дума (Khazad-dûm) или Мории — огромного подземного королевства гномов в Мглистых горах Средиземья из трилогии Дж. Р. Р. Толкиена «Властелин колец».[1]
См. также
Примечания
- ↑ 1 2 3 4 5 6 7 8 Paulo Sérgio L. M. Barreto, Vincent Rijmen. The Khazad Block Cipher. www.larc.usp.br. Дата обращения: 30 ноября 2016. Архивировано из оригинала 1 декабря 2016 года.
- ↑ 1 2 3 4 Панасенко С. П. Алгоритмы шифрования. Специальный справочник.. — СПб.: БХВ-Петербург, 2009. — С. 282—287. — 576 с. — ISBN 978-5-9775-0319-8.
- ↑ 1 2 Lars R. Knudsen, Matthew J.B. Robshaw. The Block Cipher Companion. — Springer, 2011. — С. 63. — 267 с. — ISBN 978-3-642-17341-7.
- ↑ Joan Daernen, Vincent Rijrnen. The Design of Rijndael. — Springer, 2002. — С. 160. — 238 с. — ISBN 3-540-42580-2.
- ↑ 1 2 Описание шифра Khazad для первого этапа конкурса NESSIE. Дата обращения: 2 декабря 2016. Архивировано 6 мая 2021 года.
- ↑ Paulo S.L.M. Barreto and Vincent Rijmen. The KHAZAD Legacy-Level Block Cipher. Архивировано 23 февраля 2012 года.
- ↑ Frédéric Muller. A new attack against khazad // in Proceedings of ASIACRYPT 2003. — С. 347–358. Архивировано 6 марта 2016 года.
Литература
- Панасенко С. П. Алгоритмы шифрования. Специальный справочник. —СПб.: БХВ-Петербург, 2009. — 576 с.: ил. ISBN 978-5-9775-0319-8
Ссылки
- Официальная страница шифра KHAZAD
- Paulo S.L.M. Barreto and Vincent Rijmen. The KHAZAD Legacy-Level Block Cipher (tweaked, KHAZAD). In First Open NESSIE Workshop, KU-Leuven, 2000. Modificated submission to NESSIE selected for 2nd Phase.
- Paulo S.L.M. Barreto and Vincent Rijmen. The KHAZAD Legacy-Level Block Cipher (original, KHAZAD-0). Original submission to NESSIE.
- Alex Biryukov. Analysis of Involutional Ciphers: Khazad and Anubis. In T. Johansson, editor, Fast Software Encryption — 2003, Lectures Notes in Computer Science. Springer, 2003.
- Frédéric Muller. A New Attack against Khazad. Advances in Cryptology
- List of NESSIE submissions as originally submitted
- Modifications to NESSIE submissions selected for 2nd Phase
- Deliverables of the NESSIE project
- NESSIE Public Report D14: Report on the Performance Evaluation of NESSIE Candidates I
- NESSIE Public Report D18: Update on the selection of algorithms for further investigation during the second round.










![{\displaystyle (\sigma [k_{8}]\circ \gamma )\circ (\sigma [k_{7}]\circ \theta \circ \gamma )\circ ...\circ (\sigma [k_{1}]\circ \theta \circ \gamma )\circ \sigma [k_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81524f09039bf4c6d998cce350c07ed815a09871)
![{\displaystyle (\sigma [k_{0}]\circ \gamma )\circ (\sigma [\theta (k_{1})]\circ \theta \circ \gamma )\circ ...\circ (\sigma [\theta (k_{7})]\circ \theta \circ \gamma )\circ \sigma [k_{8}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/912cca7c2824016d8f493e78fdc7b17a9c5ea156)
![{\displaystyle \rho [k]=\sigma [k]\circ \theta \circ \gamma }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e11ac59adce3ef20a22c227025d8adf0574e2cc0)










![{\displaystyle \sigma [k_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/669c7e53e87b4e2087822bfcb2c3febb036677aa)
















![{\displaystyle S[x]=(s_{0}(x),...,s_{n-1}(x))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4a06e470de1e7de7ab0d9ab42374c51aef6e89)





![{\displaystyle \delta _{S}\equiv 2^{-n}\cdot \max _{a\neq 0,b}\{c\in GF(2^{n})\mid S[c\oplus a]\oplus S[c]=b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96a489750e394fa3f16d668c0a68703f1b5d9cb5)