Великая теорема Ферма́ — одна из самых популярных теорем математики. Сформулирована французским математиком Пьером Ферма в 1637 году. Несмотря на простоту формулировки, буквально, на «школьном» арифметическом уровне, доказательство теоремы искали многие математики на протяжении более трёхсот лет. И только в 1994 году теорема была доказана английским математиком Эндрю Уайлсом с коллегами; публикация доказательства состоялась в 1995 году.
Те́ст Люка́ — Ле́мера — полиномиальный, детерминированный и безусловный тест простоты для чисел Мерсенна. Сформулирован Эдуардом Люка в 1878 году и доказан Лемером в 1930 году.
Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Основна́я теоре́ма а́лгебры — утверждение о том, что поле комплексных чисел алгебраически замкнуто, то есть что всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел. Утверждение справедливо и для многочленов с вещественными коэффициентами, так как всякое вещественное число является комплексным с нулевой мнимой частью.
Теоре́ма о модуля́рности — математическая теорема, устанавливающая важное соотношение между эллиптическими кривыми над полем рациональных чисел и модулярными формами, являющимися определёнными аналитическими функциями комплексного переменного. В 1995 году Эндрю Уайлс, не без помощи Ричарда Тейлора, доказал данную теорему для всех полустабильных эллиптических кривых над полем рациональных чисел. Доказательство остальных (неполустабильных) случаев теоремы явилось результатом работ Кристо́фа Брёйля, Брайана Конрада, Фреда Даймонда и Ричарда Тейлора. До 2001 года теорема называлась гипотезой Таниямы — Шимуры — Вейля.
Доказа́тельство с нулевы́м разглаше́нием (информа́ции) в криптографии — интерактивный криптографический протокол, позволяющий одной из взаимодействующих сторон убедиться в достоверности какого-либо утверждения, не имея при этом никакой другой информации от второй стороны. Причём последнее условие является необходимым, так как обычно доказать, что сторона обладает определёнными сведениями в большинстве случаев тривиально, если она имеет право просто раскрыть информацию. Вся сложность состоит в том, чтобы доказать, что у одной из сторон есть информация, не раскрывая её содержания. Протокол должен учитывать, что доказывающий сможет убедить проверяющего только в случае, если утверждение действительно доказано. В противном случае сделать это будет невозможно, или крайне маловероятно из-за вычислительной сложности.
Coq — интерактивное программное средство доказательства теорем, использующее собственный язык функционального программирования (Gallina) с зависимыми типами. Позволяет записывать математические теоремы и их доказательства, удобно модифицировать их, проверяет их на правильность. Пользователь интерактивно создаёт доказательство сверху вниз, начиная с цели. Coq может автоматически находить доказательства в некоторых ограниченных теориях с помощью так называемых тактик. Coq применяется для верификации программ.
Теорема о классификации простых конечных групп — теорема теории групп, классифицирующая с точностью до изоморфизма простые конечные группы.
Теорема Кронекера — Вебера — утверждение в алгебраической теории чисел, согласно которому каждое конечное абелево расширение поля рациональных чисел 
, или, другими словами, каждое алгебраическое числовое поле, чья группа Галуа над является абелевой, — является подполем некоторого кругового поля, то есть поля, полученного присоединением корня из единицы к рациональным числам.
Теорема Евклида — основной элемент теории чисел. Она утверждает, что для любого конечного списка простых чисел найдётся простое число, не вошедшее в этот список.
Теорема ван дер Вардена — классический результат комбинаторной теории чисел об одноцветных арифметических прогрессиях в раскрасках натуральных чисел. Теорема является типичным утверждением теории Рамсея, а также предтечей теоремы Семереди, которая положила начало большой ветви аддитивной комбинаторики.
Теорема Ферма о многоугольных числах утверждает, что любое натуральное число представимо как сумма не более 
-угольных чисел.
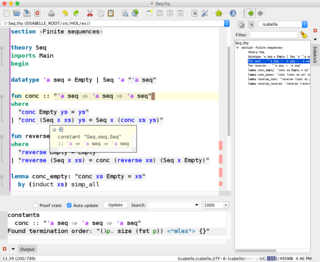
Isabelle — интерактивный инструмент для автоматического доказательства, использующий логику высшего порядка. Реализован в том же стиле, что и один из первых подобных инструментов — LCF и, точно так же как и LCF, был первоначально полностью написан на языке Standard ML. Система содержит компактное логическое ядро, которое можно принимать в качестве истинного без дополнительных доказательств. Как универсальный инструмент, реализует металогику, которая используется для реализации нескольких вариантов логики объектов Isabelle, таких как логика первого порядка (FOL), логика высшего порядка (HOL) или теория множеств Цермело-Френкеля (ZFC). Чаще всего используется вариант объектной логики является Isabelle/HOL, так же достаточно серьёзные разработки в области теории множеств проводились с использованием Isabelle/ZF.
Инструмент интерактивного доказательства теорем — программное обеспечение, помогающее исследователю в разработке формальных доказательств. Доказательства вырабатываются в процессе взаимодействия человека с машиной. Как правило, такое программное обеспечения включает в себя какую-то разновидность интерактивного редактора доказательств или другой интерфейс, с помощью которого человек может вести поиск доказательств, сведения о которых хранятся в компьютере, а также процедуры автоматической проверки доказательств, осуществляемые компьютером.
Тригонометрическая сумма — это конечная сумма комплексных чисел, геометрически соответствующих векторам на единичной окружности, то есть вида 
Metamath — очень простой формальный язык и соответствующая ему компактная компьютерная программа для формализации, коллекционирования в архиве соответствующего сайта, подтверждения и изучения математических доказательств. Существует несколько баз данных доказанных теорем, разработанных используя Metamath, начиная с классических результатов в логике, теории множеств, теории чисел, алгебре, топологии, анализе и других разделах математики. Данный проект первый в своём роде, который позволяет удобно и интерактивно исследовать свою базу данных формализированных теорем в формате обыкновенного сайта.
