ROC-кривая
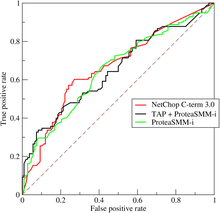
ROC-кривая (англ. receiver operating characteristic, рабочая характеристика приёмника) — график, позволяющий оценить качество бинарной классификации, отображает соотношение между долей объектов от общего количества носителей признака, верно классифицированных как несущие признак (англ. true positive rate, TPR, называемой чувствительностью алгоритма классификации), и долей объектов от общего количества объектов, не несущих признака, ошибочно классифицированных как несущие признак (англ. false positive rate, FPR, величина 1-FPR называется специфичностью алгоритма классификации) при варьировании порога решающего правила.
Также известна как кривая ошибок. Анализ классификаций с применением ROC-кривых называется ROC-анализом.
Количественная интерпретация ROC даёт показатель AUC (англ. Area Under Curve, площадь под кривой) — площадь, ограниченная ROC-кривой и осью доли ложных положительных классификаций. Чем выше показатель AUC, тем качественнее классификатор, при этом значение 0,5 демонстрирует непригодность выбранного метода классификации (соответствует случайному гаданию). Значение менее 0,5 говорит, что классификатор действует с точностью до наоборот: если положительные назвать отрицательными и наоборот, классификатор будет работать лучше.
Основная концепция
Злокачественные опухоли — классическое приложение задач классификации: симптомы часто появляются, когда болезнь запущена до неизлечимости, а надёжные тесты крайне дороги. Потому востребованы дешёвые, хоть и не столь надёжные, тесты — а мы будем объяснять на примере здоровых и больных.
Задача классификации состоит в том, чтобы относить ранее неизвестные объекты к тому или иному классу. Примером такой задачи может быть диагностика болезни — заболел пациент (положительный результат) или нет (отрицательный результат). Тогда в результате классификации может наблюдаться четыре различных ситуации:
- истинно-положительный результат (true-positive, TP) — пациент больной, диагноз положительный;
- ложно-положительный результат (false-positive, FP) — пациент здоров, диагноз положительный;
- истинно-отрицательный результат (true-negative, TN) — пациент здоров, диагноз отрицательный;
- ложно-отрицательный результат (false-negative, FN) — пациент больной, диагноз отрицательный.
Четыре возможных выхода могут быть сформулированы и оформлены в виде таблицы сопряжённости размера 2×2.
Тогда значение Sen=TP/(TP+FN), способность алгоритма «видеть» больных, называется чувствительность или частота истинно-положительных, Spe=TN/(TN+FP) — специфичность или частота истинно-отрицательных, способность алгоритма не принимать здоровых за больных. Экономический эффект от этих ошибок разный: ложно-отрицательный больной придёт с запущенной болезнью, на дообследование ложно-положительного будут потрачены ресурсы. Величина 1−Spe=FP/(TN+FP) называется частота ложно-положительных.
Часто классификатор выдаёт не бит «здоров-болен», а число из непрерывной шкалы: например, 0=«явно здоров», 25=«скорее всего, здоров», 50=«неопределённо», 75=«скорее всего, больной», 100=«явно больной». Но всё равно набор принимаемых решений обычно конечный, а то и бинарный: отправлять ли пациента на дообследование? Должен ли сработать толкатель, сбрасывающий деталь в контейнер с браком? Варьируя порог срабатывания, мы меняем характеристики чувствительности и специфичности: чем выше одна, тем ниже другая.
В результате изменения порога от −∞ до ∞ и нанесения точек X=1−Spe и Y=Sen в пространстве координат X,Y получается график, который и называется ROC-кривой. При пороге −∞ классификатор относит всех пациентов к больным (1−Spe=1, Sen=1). При пороге +∞ все классифицируются как здоровые (1−Spe=0, Sen=0). Потому ROC-кривая всегда идёт от (0,0) до (1,1).
Случай непрерывных случайных величин
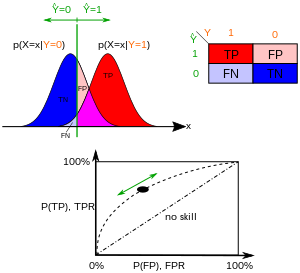
Классификация часто основывается на непрерывных случайных величинах. В этом случае удобно записать вероятность принадлежности к тому или иному классу в виде функции распределения вероятностей, зависящей от некоего порогового (граничного) значения параметра в виде , а вероятность непринадлежности как . Тогда количество ложно-положительных (false-positive rate, FPR) решений можно выразить в виде . В то же время количество истинно-положительных решений (true-positive rate, TPR) можно выразить в виде . При построении ROC-кривой по оси откладывают и по оси — , полученных при разных значениях параметра .
Например, представим, что уровни какого-нибудь белка в крови распределены нормально с центрами, равными 1 г/дЛ и 2 г/дЛ у здоровых и больных людей соответственно. Медицинский тест может давать показатель уровня какого-либо белка в плазме крови. Уровень белка выше определённой границы может рассматриваться как признак заболевания. Исследователь может сдвигать границу (черная вертикальная линия на рисунке), что приведет к изменению числа ложно-положительных результатов. Результирующий вид ROC-кривой зависит от степени пересечения двух распределений.
Частные случаи
Если генеральная совокупность конечная (что обычно и бывает на реальных наборах данных), то при движении порога t от −∞ до ∞ возможны следующие ситуации:
- Если при увеличении t количества ложно-положительных и истинно-положительных оценок объектов не изменяются, то, соответственно, значения Sen и Spe также не изменяются, и ни одной новой точки ROC-кривой не появляется, построенная часть ROC-кривой остаётся прежней.
- При увеличении t оценки одного или нескольких объектов переходят из ложно-положительных в истинно-отрицательные, а количество истинно-положительных не меняется. Соответственно, значение Sen остаётся прежним, Spe увеличивается, X = 1 − Spe уменьшается, к кривой добавляется горизонтальный отрезок.
- При увеличении t оценки одного или нескольких объектов переходят из истинно-положительных в ложно-отрицательные, а количество ложно-положительных не меняется. Тогда Y = Sen уменьшается, и к кривой добавляется вертикальный отрезок.
- Если происходит одновременно второе и третье, уменьшаются X = 1 − Spe и Y=Sen, и к ROC-кривой добавляется соответствующий наклонный отрезок.
Поскольку вероятность четвёртого события мала, ROC-кривая конечной генеральной совокупности имеет ступенчатый вид, с небольшим количеством наклонных отрезков там, где погрешности сбора и обработки данных дали одинаковый результат на объектах разных классов.
Соответственно, алгоритм построения ROC-кривой для конечной генеральной совокупности таков. Упорядочим объекты по значению критерия. Берём набор объектов с равным значением критерия, пересчитываем Sen и Spe, и рисуем отрезок. Продолжаем, пока объекты не кончатся.
ROC-кривая бинарного классификатора, выдающего 0 или 1 (например, решающего дерева), выглядит как два отрезка (0,0) → (1−Spe,Sen) → (1,1).
В идеальном случае, когда классификатор полностью разделяет положительные и отрицательные члены генеральной совокупности, сначала все ложно-положительные становятся истинно-отрицательными (отрезок (1,1)—(0,1)), затем — все истинно-положительные становятся ложно-отрицательными (отрезок (0,1)—(0,0)). То есть ROC-кривая идеального классификатора, независимо от того, какие цифры выдаёт критерий и конечна ли генеральная совокупность, выглядит как два отрезка (0,0)—(0,1)—(1,1).
При тех пороговых t, где ROC-кривая ниже диагонали 1−Spe = Sen, можно инвертировать критерий (всё, что меньше t, объявить положительным), и классификатор будет действовать лучше, чем изначально: повышается и чувствительность, и специфичность.
Применение
ROC-кривые впервые использованы в теории обработки сигналов в США во время Второй мировой войны для повышения качества распознавания объектов противника по радиолокационному сигналу[1]. После атаки на Перл Харбор в 1941 году, американские военные начали новые исследования, направленные на попытки увеличения точности опознавания японских самолетов по радиолокационным сигналам.
Впоследствии широкое применение ROC-кривые получили в медицинской диагностике[2][3]. ROC-кривые используется в эпидемиологии и медицинских исследованиях, часто упоминаются в одном контексте с доказательной медициной. В радиологии ROC-кривые используются для проверки и тестирования новых методик[4]. В социальных науках ROC-кривые используются для того, чтобы делать суждения о качестве вероятностных моделей. Также кривые используются в вопросах управления качеством продукции и кредитном скоринге.
ROC-кривые широко используются в машинном обучении. Впервые в этом контексте они были использованы в работе 1989 года, где продемонстрировано применение ROC-кривых при сравнении нескольких алгоритмов классификации[5].
Дополнительные варианты использования
Площадь под кривой
В нормированном пространстве площадь под кривой (AUC — Area Under Curve, AUROC — Area Under Receiver Operating Characteristic) эквивалентна вероятности, что классификатор присвоит больший вес случайно выбранной положительной сущности, чем случайно выбранной отрицательной.[6] Это может быть показано следующим образом: площадь под кривой задаётся интегралом (ось развёрнута со знаком минус — большему значению координаты соответствует меньшее значение параметра ): . Угловые скобки обозначают операцию взятия среднего.
Было показано, что AUC тесно связана с U-критерием Манна — Уитни[7][8], который является показателем того, присваивается ли позитивным элементам больший вес, чем негативным. Величина AUC также связана с Критерием Уилкоксона[8] и с коэффициентом Джини () следующим образом: , где:
[9].
Показатель AUC также часто используется для того, чтобы сравнивать модели, полученные на основе обучающей выборки[10]. Однако, в некоторых случаях использование этого показателя затруднено тем, что AUC является чувствительным к шуму[11]. Также в некоторых работах отмечаются дополнительные проблемы, возникающие при использовании величины AUC для сравнения моделей[12][13]. Как уже было отмечено ранее, величина площади под кривой может быть использована как величина вероятности, с которой случайно выбранной позитивной сущности будет присвоен вес больший, чем случайно выбранной негативной. Однако, в ряде работ[11][12] выдвинуты предположения о сложности получения надежных оценок величин AUC. Так, практическая ценность показателя AUC была поставлена под сомнение[13], указывая на то, что зачастую величина может вносить больше неопределенности, чем ясности.
ROC-кривые в небинарных задачах классификации
Расширение ROC-кривых на случай задач классификации с более чем двумя классами всегда было сопряжено с трудностями, так как количество степеней свободы растет квадратично от количества классов, и ROC-пространство имеет измерений, где — количество классов.[14] Также были развиты некоторые практические подходы для случая, когда количество классов равно трем.[15] Объем под ROC-поверхностью (VUS — Volume Under Surface) рассматривается как метрика качества классификаторов для небинарных задач классификации.[16] Однако, из-за сложности анализа переменной VUS, были развиты другие подходы[17], основанные на расширении понятия VUS.
В связи с успешным применением ROC-кривых для анализа качества классификаторов, были изучены расширения ROC-кривых для других задач обучения с учителем. Среди работ стоит отметить посвященные так называемым REC-кривым (regression error characteristic — REC-curve)[18] и RROC-кривым (Regression ROC curves)[19]. Стоит отметить, что площадь под RROC-кривой пропорциональна дисперсии ошибки регрессионной модели.
Примечания
- ↑ Green, David M.; Swets, John A. Signal detection theory and psychophysics (англ.). — New York, NY: John Wiley and Sons Inc., 1966. — ISBN 0-471-32420-5.
- ↑ Zweig, Mark H.; Campbell, Gregory. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine (англ.) // Clinical Chemistry : journal. — 1993. — Vol. 39, no. 8. — P. 561—577. — PMID 8472349. Архивировано 23 сентября 2015 года.
- ↑ Pepe, Margaret S. The statistical evaluation of medical tests for classification and prediction (англ.). — New York, NY: Oxford, 2003. — ISBN 0-19-856582-8.
- ↑ Obuchowski, Nancy A. Receiver operating characteristic curves and their use in radiology (англ.) // Radiology : journal. — 2003. — Vol. 229, no. 1. — P. 3—8. — doi:10.1148/radiol.2291010898. — PMID 14519861.
- ↑ Spackman, Kent A. (1989). "Signal detection theory: Valuable tools for evaluating inductive learning". Proceedings of the Sixth International Workshop on Machine Learning. San Mateo, CA: Morgan Kaufmann. pp. 160—163.
- ↑ Fawcett, Tom (2006); An introduction to ROC analysis, Pattern Recognition Letters, 27, 861—874.
- ↑ Hanley, James A.; McNeil, Barbara J. The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve (англ.) // Radiology : journal. — 1982. — Vol. 143. — P. 29—36. — PMID 7063747.
- ↑ 1 2 Mason, Simon J.; Graham, Nicholas E. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation (англ.) // Quarterly Journal of the Royal Meteorological Society[англ.] : journal. — 2002. — No. 128. — P. 2145—2166. Архивировано 20 ноября 2008 года.
- ↑ Hand, David J.; and Till, Robert J. (2001); A simple generalization of the area under the ROC curve for multiple class classification problems, Machine Learning, 45, 171—186.
- ↑ Hanley, James A.; McNeil, Barbara J. A method of comparing the areas under receiver operating characteristic curves derived from the same cases (англ.) // Radiology : journal. — 1983. — 1 September (vol. 148, no. 3). — P. 839—843. — PMID 6878708. Архивировано 5 сентября 2008 года.
- ↑ 1 2 Hanczar, Blaise; Hua, Jianping; Sima, Chao; Weinstein, John; Bittner, Michael; and Dougherty, Edward R. (2010); Small-sample precision of ROC-related estimates, Bioinformatics 26 (6): 822—830
- ↑ 1 2 Lobo, Jorge M.; Jiménez-Valverde, Alberto; and Real, Raimundo (2008), AUC: a misleading measure of the performance of predictive distribution models, Global Ecology and Biogeography, 17: 145—151
- ↑ 1 2 Hand, David J. (2009); Measuring classifier performance: A coherent alternative to the area under the ROC curve, Machine Learning, 77: 103—123
- ↑ Srinivasan, A. (1999). "Note on the Location of Optimal Classifiers in N-dimensional ROC Space". Technical Report PRG-TR-2-99, Oxford University Computing Laboratory, Wolfson Building, Parks Road, Oxford.
- ↑ Mossman, D. Three-way ROCs // Medical Decision Making. — 1999. — Т. 19. — С. 78—89. — doi:10.1177/0272989x9901900110.
- ↑ Ferri, C.; Hernandez-Orallo, J.; Salido, M.A. (2003). "Volume under the ROC Surface for Multi-class Problems". Machine Learning: ECML 2003. pp. 108–120.
- ↑ Till, D.J.; Hand, R.J. A Simple Generalisation of the Area Under the ROC Curve for Multiple Class Classification Problems (англ.) // Machine Learning : journal. — 2012. — Vol. 45. — P. 171—186.
- ↑ Bi, J.; Bennett, K.P. (2003). "Regression error characteristic curves". Twentieth International Conference on Machine Learning (ICML-2003). Washington, DC.
- ↑ Hernandez-Orallo, J. ROC curves for regression // Pattern Recognition. — 2013. — Т. 46, № 12. — С. 3395—3411 .. — doi:10.1016/j.patcog.2013.06.014.