Timsort

Timsort — гибридный алгоритм сортировки. Гибридный, потому что сочетает сортировку вставками и сортировку слиянием. Опубликован в 2002 году Тимом Петерсом. В настоящее время является стандартным алгоритмом^[1] сортировки в Python, OpenJDK 7^[2], Apple Swift Standard Library 5^[3] и реализован в Android JDK 1.5^[4]. Основная идея алгоритма заключается в использовании наблюдения, согласно которому на практике сортируемые (упорядочиваемые) массивы данных часто содержат отсортированные (упорядоченные) подмассивы. На таких данных алгоритм timsort сравнительно быстрее некоторых алгоритмов сортировки^[5].

Работу алгоритма можно разделить на следующие шаги:

1. определение минимального размера подмассива массива;
2. деление входного массива на подмассивы с использованием специального алгоритма;
3. сортировка каждого подмассива с использованием алгоритма сортировки вставками;
4. объединение отсортированных подмассивов в массив с использованием изменённого алгоритма сортировки слиянием.

Особенности алгоритма заключаются в особенностях алгоритма деления массива на подмассивы и в особенностях изменённого алгоритма сортировки слиянием.

N — размер входного массива.

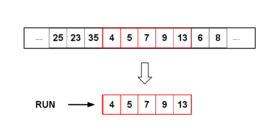
run — отсортированный (упорядоченный) подмассив входного массива. ${\displaystyle a_{i}}$ — i-й элемент упорядоченного подмассива. Упорядочение возможно двумя способами:

• либо нестрого по возрастанию: ${\displaystyle a_{0}\leqslant a_{1}\leqslant a_{2}\leqslant ...}$;
• либо строго по убыванию: ${\displaystyle a_{0}>a_{1}>a_{2}>...}$.

minrun — минимальный размер подмассива входного массива, минимальный размер упорядоченной последовательности. Рассчитывается по определённой логике из числа N на первом шаге алгоритма и используется на втором шаге алгоритма при делении входного массива на подмассивы.

Число minrun (минимальный размер упорядоченного подмассива) определяется на основе числа N, исходя из следующих принципов.

(1) Подмассив размера minrun будет сортироваться с использованием алгоритма сортировки вставками. Алгоритм сортировки вставками эффективен только для сравнительно небольших массивов. То есть, число minrun ограничено сверху, должно быть таким, чтобы алгоритм сортировки вставками был эффективным.

(2) Два подмассива размера minrun будут объединяться с использованием алгоритма сортировки слиянием. Для алгоритма сортировки слиянием верно, что, чем меньше сортируемый массив (то есть, чем меньше число minrun), тем больше итераций слияния подмассивов придётся выполнить на последнем шаге алгоритма. То есть, число minrun ограничено снизу, должно быть таким, чтобы алгоритм сортировки слиянием был эффективным. Алгоритм сортировки слиянием подмассивов эффективнее работает с подмассивами примерно равного размера. Поэтому оптимальная величина для N / minrun равна либо степени числа 2, либо близка к ней.

Эксперименты, проведённые автором алгоритма timsort, показали следующее:

• если minrun > 256, то становится не эффективным алгоритм сортировки вставками;
• если minrun < 8, то становится не эффективным алгоритм сортировки слиянием;
• наиболее эффективно использовать minrun из отрезка [32;64];
• если N < 64, то minrun = N. Тогда создаётся один подмассив. Подмассив сортируется алгоритмом сортировки вставками. Так как подмассив один, алгоритм сортировки слиянием не применяется. Алгоритм timsort превращается в алгоритм сортировки вставками.

В данный момент алгоритм расчёта minrun следующий:

• взять старшие 6 бит числа N;
• если в оставшихся младших битах числа N имеется хотя бы один ненулевой бит, увеличить полученное число на единицу.

Реализуем на языке Java метод «getMinrun()» для расчёта числа minrun.

    public static int getMinrun(int n) {
        // n = N, размер входного массива.
        int r = 0;
        // 2^6 = 64.
        while (n >= 64) {
            r |= (n & 1);
            // Если среди младших битов n имеется хотя бы один ненулевой бит, переменная r станет равна 1.
            n >>= 1;
        }
        // Теперь переменная n содержит старшие 6 бит N.
        return n + r; // minrun
    }

Для реализации шагов 2 и 3 выполняются следующие действия.

• Указатель текущего элемента ставится в начало входного массива.
• Начиная с текущего элемента, во входном массиве ищется упорядоченный подмассив run. По определению в подмассив run войдет текущий элемент и элемент, следующий за текущим. Если получившийся подмассив run упорядочен по убыванию, элементы переставляются так, чтобы подмассив стал упорядочен по возрастанию.
• Если размер текущего подмассива run (size(run)) меньше числа minrun, подмассив run увеличивается на (minrun-size(run)) элементов, следующих за подмассивом run. В результате на выходе получается подмассив run либо размером minrun, либо размером, большим minrun. Часть подмассива run (а в идеальном случае — весь подмассив) будет упорядочена.
• К подмассиву run применяется алгоритм сортировки вставками. Так как размер подмассива run сравнительно невелик и часть подмассива уже упорядочена, алгоритм сортировки вставками сработает быстро и эффективно.
• Указатель текущего элемента ставится на элемент, следующий за подмассивом run.
• Если конец входного массива не достигнут, выполняется переход к пункту 2. Иначе, завершается выполнение данного шага.

Если входной массив содержал случайные данные, размер упорядоченных подмассивов будет близок к minrun. Если входной масив содержал упорядоченные подмассивы, упорядоченные подмассивы будут иметь размер, больший minrun. Чтобы получить упорядоченный массив (результирующий массив), требуется объединить упорядоченные подмассивы. Чтобы объединение выполнялось эффективно, должно быть верно следующее:

• должны объединяться подмассивы примерно одинакового размера;
• требуется не делать бессмысленных перестановок элементов (сохранять стабильность алгоритма).

Алгоритм:

• создание пустого стека пар <индекс начала подмассива>-<размер подмассива>. Выбор первого упорядоченного подмассива на роль текущего подмассива run;
• добавление в стек пары <индекс начала подмассива>-<размер подмассива> для текущего подмассива run;
• определение, требуется ли выполнять объединение предыдущего подмассива run и текущего подмассива run. Для этого проверка, верны ли следующие два неравенства (пусть X, Y и Z — размеры трёх верхних в стеке подмассивов):

   Z > Y + X;
   Y > X;

• если любое из неравенств ложно, объединение подмассива Y с меньшим из подмассивов X и Z. Повторение либо до тех пор, пока оба неравенства не станут верны, либо до тех пор, пока данные не станут упорядочены;
• если ещё остались не рассмотренные упорядоченные подмассивы, выбор следующего подмассива на роль текущего подмассива run и переход к пункту 2. Иначе, завершение алгоритма.

Цель этой процедуры — сохранение баланса. Изменения будут выглядеть так, как показано на картинке. А значит размеры хранимых в стеке подмассивов таковы, что алгоритм сортировки слиянием будет эффективен. В идеальном случае размеры хранимых в стеке подмассивов будут равны 128, 64, 32, 16, 8, 4, 2, 2 соответственно. Тогда объединения подмассивов не будут выполняться до тех пор, пока не встретятся два последних подмассива (подмассив размером 2 и подмассив размером 2); после чего будут выполнены 7 идеально сбалансированных объединений:

1. объединение подмассива размером 2 из стека и подмассива размером 2 из стека;
2. объединение полученного подмассива размером 4 и подмассива размером 4 из стека;
3. объединение полученного подмассива размером 8 и подмассива размером 8 из стека;
4. объединение полученного подмассива размером 16 и подмассива размером 16 из стека;
5. объединение полученного подмассива размером 32 и подмассива размером 32 из стека;
6. объединение полученного подмассива размером 64 и подмассива размером 64 из стека;
7. объединение полученного подмассива размером 128 и подмассива размером 128 из стека.

От расположения подмассивов зависит то, как процедура объединения (соединения, слияния) будет выполнять перебор (обход) и сравнение элементов подмассива. Для реализации алгоритма необходимы следующие процедуры:

• процедура перебора элементов подмассива слева направо (если меньший массив находится слева);
• процедура перебора элементов подмассива справа налево (если меньший массив находится справа).

На практике обычно реализуют процедуру перебора элементов массива слева направо и при выборе подмассива на роль левого массива не учитывают размер подмассива, так как это почти не влияет на время сортировки.

Перечислим шаги алгоритма.

1. Создаётся временный массив размером, равным размеру меньшего из объединяемых подмассивов.
2. Элементы меньшего из подмассивов копируются во временный массив.
3. Указатель текущей позиции временного массива ставится на первый (последний) элемент временного массива. Указатель текущей позиции большего подмассива ставится на первый (последний) элемент большего подмассива.
4. На каждом следующем шаге сравниваются текущий элемент большего подмассива и текущий элемент временного подмассива. Берётся меньший (больший) из двух элементов и копируется в новый (отсортированный) массив. Указатель текущего элемента того подмассива, из которого был взят элемент, перемещается на одну позицию влево (вправо).
5. Пункт 4 повторяется до тех пор, пока в одном из подмассивов не закончатся элементы.
6. Все элементы оставшегося подмассива добавляются в конец нового массива.

Пусть

A = {1, 2, ..., 10_000},
B = {20_000, 20_001, ..., 30_000}.

Рассмотрим объединение массивов A и B. Массив A содержит 10_000 элементов. Массив B содержит 10_001 элемент. На четвёртом шаге выполняется одно сравнение (элементов двух массивов) и одно копирование. 4-й шаг будет выполнен 10_000 раз. То есть, будет выполнено 10_000 сравнений и 10_000 копирований. Алгоритм timsort предлагает изменение, называемое словом «галоп». Опишем шаги алгоритма.

• Начинается объединение, как было описано выше.
• При каждом копировании элемента (временного или большего) подмассива в результирующий массив запоминается, из какого именно подмассива копируется элемент: из временного подмассива или из большего подмассива.
• Если некоторое количество элементов (в рассматриваемом примере — 7 элементов) уже было взято из одного подмассива, предполагается, что и в дальнейшем придётся брать элементы из того же подмассива. Чтобы подтвердить предположение, алгоритм переходит в так называемый режим «галопа» (galloping mode). В режиме «галопа» алгоритм перемещается по подмассиву - претенденту на поставку следующей большой порции элементов (подмассив упорядочен) бинарным поиском текущего элемента из второго объединяемого подмассива.
• В момент, когда данные из текущего подмассива - поставщика либо перестанут подходить, либо будет достигнут конец подмассива, данные будут скопированы целиком.

Рассмотрим работу алгоритма c переходом в режима «галопа» на примере объединения массивов A и B. Первые 7 итераций сравниваются элементы 1, 2, 3, 4, 5, 6 и 7 массива A и элемент 20_000 массива B. Так как элемент 20_000 массива B больше первых семи элементов массива A, элементы массива A копируются в результирующий массив. В данном примере считается, что для перехода в режим «галопа» требуется подряд взять из одного из массивов 7 элементов. Так как из массива A было взято 7 элементов подряд, начиная со следующей итерации, алгоритм переходит в режим «галопа». Элемент 20_000 массива B последовательно сравнивается с элементами 8, 10, 14, 22, 38, n+2^i, …, 10_000 массива A. Всего выполняется примерно log_2(N) сравнений. После того, как будет достигнут конец массива A, станет известно, что любые элементы массива A меньше любых элементов массива B. Нужные элементы из массива A копируются в результирующий массив.

• Peter McIlroy "Optimistic Sorting and Information Theoretic Complexity", Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, ISBN 0-89871-313-7, Chapter 53, pp 467-474, January 1993. [1]
• Magnus Lie Hetland. Python Algorithms: Mastering Basic Algorithms in the Python Language. — Apress, 2010. — 336 с. — ISBN 978-1-4302-3237-7.

• Представление алгоритма от его создателя (англ.). Архивировано 4 сентября 2012 года.
• Timsort, реализованный на Python для PyPy (англ.) (py). Архивировано 4 сентября 2012 года.
• Визуализация алгоритма (англ.). Архивировано 4 сентября 2012 года.
• Визуализация алгоритма tim sort на YouTube.
• Реализация Timsort на C++ 29 мая 2024 года.