XTEA

XTEA
XTEA
Создатель	Дэвид Уилер[англ.]и Роджер Нидхем
Создан	1997 г.
Опубликован	1997 г.
Размер ключа	128 бит
Размер блока	64 бит
Число раундов	64
Тип	Сеть Фейстеля

В криптографии, XTEA (eXtended TEA) — блочный шифроалгоритм, призванный устранить критические ошибки алгоритма TEA. Разработчиками шифра являются Дэвид Уилер^[англ.] и Роджер Нидхем (факультет компьютерных наук Кэмбриджского университета). Алгоритм был представлен в неизданном техническом отчете в 1997 году^[1]. Шифр не патентован, широко используется в ряде криптографических приложений и широком спектре аппаратного обеспечения благодаря крайне низким требованиям к памяти и простоте реализации.

Свойства шифра

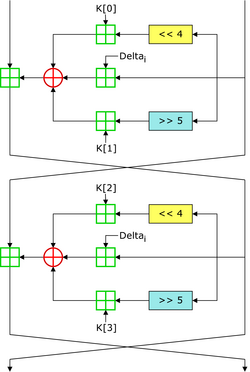
Как и TEA, шифр основан на операциях с 64-битным блоком, имеет 32 полных цикла, в каждом полном цикле по два раунда Сети Фейстеля, что означает 64 раунда сети Фейстеля. Однако, число раундов для достижения лучшей диффузии может быть увеличено в ущерб производительности. Кроме того в XTEA, как и в TEA, используется 128-битный ключ, состоящий из четырёх 32-битных слов K[0], K[1], K[2] и K[3]. В XTEA нет алгоритма планирования ключей в привычном понимании. Для того, чтобы определить какое из четырёх слов ключа использовать в каждом раунде, в алгоритме используется константа δ = 9E3779B9₁₆. В TEA же такого распределения нет. Ещё одним отличием от TEA является перестановка битовых операций, использующихся в шифре. Благодаря этим улучшениям XTEA не претерпел сильных усложнений по сравнению с TEA, но в то же время ликвидировал два основных недостатка алгоритма TEA^[1]:

каждый ключ в TEA эквивалентен трем другим, что означает, что эффективная длина ключа составляет 126 бит вместо 128, как это было задумано разработчиками;
TEA восприимчив к атакам на связанных ключах. Такая атака может потребовать всего лишь 2²³ выбранного открытого текста и иметь временную сложность равную 2³²^[2].

Описание алгоритма

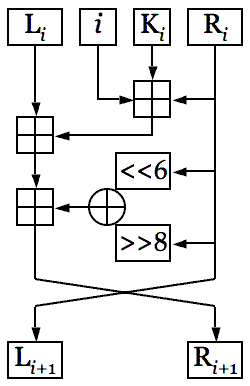
В работе XTEA применяются следующие логические операции: исключающее «ИЛИ», битовый сдвиг и логическое «И». Кроме того в XTEA используется операция сложения целых чисел по модулю 2³², обозначающаяся как x $\boxplus$ y (x и y $\in$ Z_2³²). Исключающее «ИЛИ» в булевой логике обозначается как x $\oplus$ y, а в языке Си как x ^ y. Логическое «И» в булевой логике — x $\land$ y в языке Си — x & y. Логический сдвиг x на y бит влево обозначается как x $\ll$ y, а логический сдвиг x на y бит вправо обозначается как x $\gg$ y. Пусть на вход n-го (1 ≤ n ≤ 64) раунда алгоритма подается (L_n,R_n), а на выходе получается (L_n+1,R_n+1), причем L_n+1 = R_n. R_n+1 вычисляется следующим образом:

если n = 2 * i — 1 для 1 ≤ i ≤ 32, то R_n+1 = L_n + ({ (R_n $\ll$ 4 $\oplus$ R_n $\gg$ 5) $\boxplus$ R_n } $\oplus$ ({ i — 1 } * δ $\boxplus$ K [ ({ i — 1 } * δ) $\land$ 3 ]),

если n = 2 * i для 1 ≤ i ≤ 32, то R_n+1 = L_n + ({ (R_n $\ll$ 4 $\oplus$ R_n $\gg$ 5) $\boxplus$ R_n } $\oplus$ (i * δ $\boxplus$ K [ (i * δ $\gg$ 11) $\land$ 3 ]).

Так как это блочный шифроалгоритм, где длина блока 64-бит, а длина данных может быть не кратна 64-битам, значения всех байтов дополняющих блок до кратности в 64-бит устанавливается в 0x01 .

Криптоанализ алгоритма

Считается что XTEA более защищен, чем ТEA, однако можно подобрать такой тип атак для которых XTEA более уязвим^[3]. Первый подход — это дифференциальные атаки. Так как TEA использует сложение по модулю 2³² ключа раунда и открытого текста, подающегося на вход, а XTEA использует исключающее «ИЛИ», то проще проводить дифференциальную атаку на XTEA, чем на TEA. После 14 раундов XTEA можно построить с вероятностью 2^−57.79 дифференциальную характеристику и использовать её для взлома XTEA включающего в себя 16 раундов (данная атака требует 2⁶¹ выбранных открытых текстов). В то же время для TEA затруднительно построить хорошую дифференциальную характеристику. Второй подход усеченная дифференциальная атака. После 8 раундов TEA и XTEA можно построить усеченную дифференциальную характеристику с вероятностью 1. Посредством данной атаки можно взломать XTEA с максимальным количеством раундов — 23 и TEA с максимальным количеством раундов — 17. Такое различие наблюдается из-за свойств планирования ключей в каждом из алгоритмов.

Наиболее успешная из опубликованных атак на XTEA — это дифференциальная атака на связанных ключах, которая способна взломать 37 из 64 раундов алгоритма, используя 2⁶³ выбранных открытых текстов с временной сложностью 2¹²⁵. Если рассматривать подмножество слабых ключей, в которое входят 2^107.5 ключей из 2¹²⁸, то эта жа атака способна взломать 51 из 64 раундов алгоритма с временной сложностью 2¹²³^[4].

Пример реализации алгоритма

Реализация на языке Си (адаптированный вариант кода, представленного в статье Дэвида Уилера и Роджера Нидхэма^[1]) шифрования и расшифрования с использованием алгоритма XTEA:

#include <stdint.h>

void xtea_encipher(unsigned int num_rounds, uint32_t *v, uint32_t const *k) {
    unsigned int i;
    uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;
    for (i=0; i < num_rounds; i++) {
        v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + k[sum & 3]);
        sum += delta;
        v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + k[(sum>>11) & 3]);
    }
    v[0]=v0; v[1]=v1;
}

void xtea_decipher(unsigned int num_rounds, uint32_t *v, uint32_t const *k) {
    unsigned int i;
    uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;
    for (i=0; i < num_rounds; i++) {
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + k[(sum>>11) & 3]);
        sum -= delta;
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + k[sum & 3]);
    }
    v[0]=v0; v[1]=v1;
}

Комментарии:

v — исходный текст состоящий из двух слов по 32 бита
k — ключ состоящий из четырёх 32-битных слов
num_rounds — число циклов алгоритма (рекомендуется 32)
num_rounds должно быть одинаковым для шифрования и расшифрования, если num_rounds==0 то ни шифрования, ни расшифрования происходить не будет

Изменения по сравнению с оригинальным кодом:

используется тип uint32_t вследствие того, что он всегда имеет размер 32 бита в отличие от long (присутствующий в оригинальном коде), который может содержать 64 бита (например в некоторых 64-битных системах)
исходный код не использует тип const
в исходном коде опущены избыточные скобки в выражениях для v0 и v1, в данной модификации они оставлены для большей наглядности

Версии алгоритма

Обнаруженные уязвимости в ключевом расписании и наличие успешных атак на алгоритмы TEA, XTEA и XXTEA привели к созданию рядом криптоаналитиков альтернативных вариантов шифра. В частности, на данный момент существуют основанные на шифрах семейства TEA алгоритмы RTEA (Шон о’Нил), Raiden (Хулио Кастро), XTEA-1, XTEA-2 и XTEA-3^[5] (Том Ст. Денис). Впрочем, данные модификации не были столь широко исследованы и не получили достаточного практического применения.

Алгоритм XTEA-1

Одна из уязвимостей XTEA состоит в том, что биты в ключе влияют на одни и те же биты в каждом раунде алгоритма. Эта проблема может быть устранена путём использования шифра, включающего в себя алгоритм расписания ключей. Планирование ключей производится динамически и не требует выделения памяти. Расписание ключей осуществляется путём циклического битового сдвига ключа на значение, зависящее от открытого текста. Алгоритм XTEA-1 реализует эту идею по усилению шифра XTEA путём незначительного изменения структуры шифра без изменения основных принципов алгоритма.

Шифр использует технологию забеливания и зависимую от данных трансформацию подключа, что затрудняет криптоанализ, поскольку исходный алгоритм содержал уязвимость — модификация определённых бит ключа отражалась на соответствующих им битах шифротекста.

Реализация XTEA-1 на языке Си:

#include <stdint.h>

uint32_t rol(uint32_t base, uint32_t shift)
{
	uint32_t res;
        /* only 5 bits of shift are significant*/
        shift &= 0x1F;
        res = (base << shift) | (base >> (32 - shift));
        return res;
}

void xtea1_encipher(unsigned int num_rounds,uint32_t *v, uint32_t const *k)
{
	unsigned int i;
	uint32_t y, z, sum=0, delta=0x9E3779B9;
	/* load and pre-white the registers */
	y = v[0] + k[0];
	z = v[1] + k[1];
	/* Round functions */
	for (i = 0; i < num_rounds; i++) 
	{
		y += ((z << 4) ^ (z >> 5)) + (z ^ sum) + rol(k[sum & 3], z);
		sum += delta;
		z += ((y << 4) ^ (y >> 5)) + (y ^ sum) + rol(k[(sum >> 11) & 3], y);
	}
	/* post-white and store registers */
	v[0] = y ^ k[2];
	v[1] = z ^ k[3];
}

void xtea1_decipher(unsigned int num_rounds,uint32_t *v, uint32_t const *k)
{
	unsigned int i;
	uint32_t y, z,delta=0x9E3779B9,sum=delta*num_rounds;
	z = v[1] ^ k[3];
	y = v[0] ^ k[2];
	for (i = 0; i < num_rounds; i++) 
	{
		z -= ((y << 4) ^ (y >> 5)) + (y ^ sum) + rol(k[(sum >> 11) & 3], y);
		sum -= delta;
		y -= ((z << 4) ^ (z >> 5)) + (z ^ sum) + rol(k[sum & 3], z);
	
	}
	v[1] = z - k[1];
	v[0] = y - k[0];
}

Функция ‘rol' выполняет циклический битовый сдвиг ключа, используя 5 младших битов переменной shift. Этот алгоритм использует только один сдвиг за раунд, что довольно эффективно и быстро работает на большинстве современных процессоров.

Алгоритм XTEA-2

Можно изменить XTEA-1 используя 128 битный блок. Полученный алгоритм требует больше раундов, но скорость шифрования у него выше чем у XTEA.

Реализация XTEA-2 на Си:

#include <stdint.h>

void xtea2_encipher(unsigned int num_rounds,uint32_t *v, uint32_t const *k){
	unsigned int i;
	uint32_t a, b, c, d, sum=0, t,delta=0x9E3779B9;
	a = v[0];
	b = v[1] + k[0];
	c = v[2];
	d = v[3] + k[1];
	for (i = 0; i < num_rounds; i++) {
		a += ((b << 4) ^ (b >> 5)) + (d ^ sum) + rol(k[sum & 3], b);
		sum += delta;
		c += ((d << 4) ^ (d >> 5)) + (b ^ sum) + rol(k[(sum >> 11) & 3], d);
		t = a; a = b; b = c; c = d; d = t;
	}
	v[0] = a ^ k[2];
	v[1] = b;
	v[2] = c ^ k[3];
	v[3] = d;
}

void xtea2_decipher(unsigned int num_rounds,uint32_t *v, uint32_t const *k){
	unsigned int i;
	uint32_t a, b, c, d, t, delta=0x9E3779B9, sum=delta*num_rounds;
	d = v[3];
	c = v[2] ^ k[3];
	b = v[1];
	a = v[0] ^ k[2];
	for (i = 0; i < num_rounds; i++) {
		t = d; d = c; c = b; b = a; a = t;
		c -= ((d << 4) ^ (d >> 5)) + (b ^ sum) + rol(k[(sum >> 11) & 3], d);
		sum -= delta;
		a -= ((b << 4) ^ (b >> 5)) + (d ^ sum) + rol(k[sum & 3], b);
	}
	v[0] = a;
	v[1] = b - k[0];
	v[2] = c;
	v[3] = d - k[1];
}

Основное преимущество этого алгоритма — это возможность шифровать большие блоки. Этот алгоритм использует те же базовые операции что и XTEA-1, но требует больше итераций. На самом деле он требует в два раза больше итераций от 32 до 64 (от 64 до 128 раундов). 48 итераций — это компромисс между скоростью и надежностью шифрования.

Алгоритм XTEA-3

Ещё одно естественное расширение XTEA-1 — это использование 256 битного ключа и более практичного 128 битного блока. Этот алгоритм требует от 32 до 64 итераций, но в то же время обеспечивает надежную защиту от атак путём полного перебора. Шифр использует технологию забеливания и реализует операции, зависимые от ключа, что затрудняет криптоанализ.

Реализация XTEA-3 на Си:

#include <stdint.h>

void xtea3_encipher(unsigned int num_rounds,uint32_t *v, uint32_t const *k)
{
	unsigned int i;
	uint32_t a, b, c, d, sum=0, t,delta=0x9E3779B9;
	sum = 0;
	a = v[0] + k[0];
	b = v[1] + k[1];
	c = v[2] + k[2];
	d = v[3] + k[3];
	for (i = 0; i < num_rounds; i++){
		a += (((b << 4) + rol (k[(sum % 4) + 4], b)) ^
			(d + sum) ^ ((b >> 5) + rol (k[sum % 4], b >> 27)));
		sum += delta;
	        c += (((d << 4) + rol (k[((sum >> 11) % 4) + 4], d)) ^
			(b + sum) ^ ((d >> 5) + rol (k[(sum >> 11) % 4], d >> 27)));
	        t = a;a = b;b = c;c = d;d = t;
	}
	v[0] = a ^ k[4];
	v[1] = b ^ k[5];
	v[2] = c ^ k[6];
	v[3] = d ^ k[7];
}
 
void xtea3_decipher(unsigned int num_rounds,uint32_t *v, uint32_t const *k)
{
    unsigned int i;
    uint32_t a, b, c, d, t,delta=0x9E3779B9,sum = delta * num_rounds;
	d = v[3] ^ k[7];
	c = v[2] ^ k[6];
	b = v[1] ^ k[5];
	a = v[0] ^ k[4];
	for (i = 0; i < num_rounds; i++){
		t = d;d = c;c = b;b = a;a = t;
		c -= (((d << 4) + rol (k[((sum >> 11) % 4) + 4], d)) ^
			(b + sum) ^ ((d >> 5) + rol (k[(sum >> 11) % 4], d >> 27)));
          	sum -= delta;
		a -= (((b << 4) + rol (k[(sum % 4) + 4], b)) ^
			(d + sum) ^ ((b >> 5) + rol (k[sum % 4], b >> 27)));
	 }
	v[3] = d - k[3];
	v[2] = c - k[2];
	v[1] = b - k[1];
	v[0] = a - k[0];
}

XTEA-3 использует 5 старших и 5 младших бит регистра открытого текста для циклического сдвига ключа, потому что статистические данные говорят о том, что эти биты наиболее подвержены изменению. Этот алгоритм так же требует как минимум 32 итерации, однако, 48 итераций — это компромиссное соотношение между скоростью и надежностью шифрования данных.

Сравнение различных версий расширения XTEA

Эти три алгоритма являются естественными расширениями TEA и XTEA. Их отличительными чертами по сравнению с оригинальными алгоритмами шифрования являются лучшее расписание ключей и больший размер блоков и/или ключей. Использование ключей, динамически зависимых от открытого текста, означает, что не существует заранее установленного порядка для использования ключей и не требуется выделение памяти. Это довольно полезное свойство, так как задача обнаружения ключей, использующихся наиболее часто, усложняется. Шифры обладают большей защищенностью к дифференциальному криптоанализу, так как биты в ключе могут влиять на любые другие биты шифротекста. Использование нелинейной алгебры (сложение по модулю 2³², исключающее «ИЛИ») эффективно против линейного криптоананлиза. Кроме того использование этих операций не вносит уязвимостей в алгоритмы.

Первый алгоритм (XTEA-1) имеет наибольшую скорость и при достаточном количестве раундов (от 32 до 64) обладает хорошей надежностью. XTEA-2 представляет собой расширение с большим размером блока, и он не более защищен чем XTEA-1. XTEA-3 — это расширение алгоритм с использованием большего размера блока и ключа. Третий вариант работает немного медленнее, но более защищен. Так как эти алгоритмы построены на базе оригинального TEA с устранением всех известных недостатков, то их можно считать достаточно надежными.

Сравнительная таблица алгоритмов:

Название алгоритма	Минимальное количество раундов	Максимальное количество раундов	Размер блока	Размер ключа
XTEA-1	32	64	64 бита	128 бит
XTEA-2	64	128	128 бит	128 бит
XTEA-3	64	128	128 бит	256 бит

Однако данные алгоритмы все равно требуют дальнейшей доработки. Первая проблема состоит в том, только младшие биты открытого текста используются для циклического битового сдвига ключа (как в XTEA-1 и XTEA-2). Вторая проблема заключается в том что ключ разделен на две подгруппы по 4 элемента, и каждая часть выражения использует только одну подгруппу (как в XTEA-3). XTEA-3 может быть расширен путём использования всех восьми элементов в обеих частях выражения. Если эти усовершенствования будут проведены, то алгоритм станет более практичным, но тогда он будет слишком сильно отличаться от оригинального TEA.

См. также

Примечания

↑ ¹ ² ³ А. Roger M. Needham and David J. Wheeler. Tea extensions Архивная копия от 20 сентября 2017 на Wayback Machine
↑ John Kelsey, Bruce Schneier, David Wagner. Related-Key Cryptanalysis of 3-WAY, Biham-DES, CAST, DES-X, NewDES, RC2, TEA (недоступная ссылка)
↑ Seokhie Hong, Deukjo Hong, Youngdai Ko, Donghoon Chang, Wonil Lee, Sangjin Lee. Differential Cryptanalysis of TEA and XTEA (недоступная ссылка)
↑ Charles Bouillaguet, Orr Dunkelman, Gaetan Leurent, and Pierre-Alain Fouque. Another Look at Complementation Properties Архивная копия от 6 июля 2017 на Wayback Machine
↑ Tom St Denis. Extended TEA Algorithms Архивная копия от 27 августа 2018 на Wayback Machine

Ссылки

David J. Wheeler and Roger M. Needham. «Correction to xtea.» Technical report, Computer Laboratory, University of Cambridge, October 1998 (PDF).
Dukjae Moon, Kyungdeok Hwang, Wonil Lee, Sangjin Lee, and Jongin Lim. «Impossible Differential Cryptanalysis of Reduced Round XTEA and TEA.» Center for Information and Security Technologies(CIST), 2004 (PDF) (недоступная ссылка).

Реализации

The Tiny Encryption Algorithm (TEA), Simon Shepherd, 24 February 2006 — Веб-страница с описанием и ссылками на различные реализации XTEA
Реализация XTEA на PHP
Реализация XTEA на Java (32 прохода)
Python XTEA Encryption (Python recipe) — Реализация XTEA на Python
Реализация XTEA на Verilog (для FPGA)
Обращение к реализации алгоритмов XTEA-1, XTEA-2, XTEA-3 на C из Python

[report-1] ¹ ² ³ А. Roger M. Needham and David J. Wheeler. Tea extensions Архивная копия от 20 сентября 2017 на Wayback Machine

[tea_crypt-2] John Kelsey, Bruce Schneier, David Wagner. Related-Key Cryptanalysis of 3-WAY, Biham-DES, CAST, DES-X, NewDES, RC2, TEA (недоступная ссылка)

[differential-3] Seokhie Hong, Deukjo Hong, Youngdai Ko, Donghoon Chang, Wonil Lee, Sangjin Lee. Differential Cryptanalysis of TEA and XTEA (недоступная ссылка)

[4] Charles Bouillaguet, Orr Dunkelman, Gaetan Leurent, and Pierre-Alain Fouque. Another Look at Complementation Properties Архивная копия от 6 июля 2017 на Wayback Machine

[extended-5] Tom St Denis. Extended TEA Algorithms Архивная копия от 27 августа 2018 на Wayback Machine

[1]

[2]

[3]

[4]

[5]

Симметричные криптосистемы
Потоковые шифры	A3 A5 A8 Decim F-FCSR Grain HC-256 KCipher-2 MICKEY MUGI PIKE Phelix RC4 Rabbit SEAL SNOW SOSEMANUK Salsa20 STRUMOK Trivium VMPC
Сеть Фейстеля	ГОСТ 28147-89 (Магма) Blowfish Camellia CAST-128 CAST-256 CIPHERUNICORN-A CIPHERUNICORN-E CLEFIA Cobra DEAL DES DESX DFC E2 EnRUPT FEAL HPC IDEA KASUMI Khafre Khufu LOKI97 MacGuffin MARS MESH MISTY1 NewDES NDS RC5 RC6 SEED Simon Sinople Skipjack SM4 Speck TEA XTEA XXTEA Raiden RTEA Triple DES Twofish
SP-сеть	Кузнечик 3-WAY ABC ARIA AES (Rijndael) Akelarre Anubis BaseKing BassOmatic BelT CRYPTON Diamond2 Grand Cru Hierocrypt-3 Hierocrypt-L1 KHAZAD Kalyna Lucifer Present Rainbow SAFER SHARK SQUARE Serpent Threefish
Другие	FROG NUSH REDOC SC2000 SHACAL CS-Cipher