
Ба́лка — сухая или с временным водотоком долина с задернованными склонами.

Выпуклая функция — функция, надграфик или подграфик которой является выпуклым множеством.

А́рка — тип архитектурной конструкции, дугообразное перекрытие проёма — пространства между двумя опорами — колоннами, пилонами. Арка, продолжающаяся в глубину, образует свод. Таким образом арка становится «направляющей» сводчатой конструкции. В истории архитектуры известны полуциркульные, стрельчатые, коробовые, возвышенные, перспективные, уплощённые, ланцетовидные, трёхлопастные и многолопастные, подковообразные, килевидные арки.
Эшер:
- Эшер — один из вариантов перевода фамилии главного героя рассказа Эдгара Аллана По «Падение дома Ашеров».
- (4444) Эшер — астероид главного астероидного пояса. Открыт в 1985 году и назван в честь Маурицио Эшера.
- (6564) Эшер — астероид, относящийся к группе астероидов пересекающих орбиту Марса.
Оптическая иллюзия, также зрительная иллюзия — ошибка в зрительном восприятии, вызванная неточностью или неадекватностью процессов неосознаваемой коррекции зрительного образа, а также физическими причинами. Причины оптических иллюзий исследуют как при рассмотрении физиологии зрения, так и в рамках изучения психологии зрительного восприятия.

Комната смеха — традиционный аттракцион в парках развлечений. Основной концепцией комнаты смеха является головоломка типа лабиринта, но в дополнение к сбивающим с толку элементом лабиринта пространственным ощущениям, визуальные ощущения также запутываются путём изготовления стен лабиринта из оптически отражающего материала, чаще всего стеклянных зеркал. Иногда каждое зеркало может быть деформировано путём искривления, придания выпуклой или вогнутой формы, чтобы передать участвующим необычное и сбивающее с толку отражение самих себя.

Бе́та-распределе́ние в теории вероятностей и статистике — двухпараметрическое семейство абсолютно непрерывных распределений. Используется для описания случайных величин, значения которых ограничены конечным интервалом.

Точка перегиба — точка плоской кривой, в которой её ориентированная кривизна меняет знак. Если кривая является графиком функции, то в этой точке выпуклая часть функции отделяется от вогнутой.

Двойственная кривая к заданной кривой на проективной плоскости — это кривая на двойственной проективной плоскости, состоящая из касательных к заданной гладкой кривой. В этом случае кривые называются взаимно двойственными (дуальными). Понятие может быть обобщено для негладких кривых и на многомерное пространство.
Мени́ск :
- Мениск — хрящевая прокладка в некоторых суставах.
- Мениск — искривлённая свободная поверхность жидкости в месте её соприкосновения с поверхностью твёрдого тела.
- Мениск — выпукло-вогнутая линза, ограниченная двумя сферическими поверхностями.
- Мениск — металлический круг, которым греки прикрывали выставленные на открытом воздухе статуи для защиты от непогоды и загрязнения птицами.

Кривая безразличия — множество всевозможных комбинаций благ, имеющих для потребителя одинаковую полезность и по отношению к выбору которых он безразличен. В простейшем двумерном случае кривую безразличия часто изображают на плоскости в виде выпуклой линии. Однако кривая имеет такой вид лишь при выполнении ряда условий. Понятие кривой безразличия восходит к Фрэнсису Эджуорту и Вильфредо Парето.

Релье́ф — что-либо выпуклое, возвышенное на плоскости, форма, очертания поверхности (территории), совокупность неровностей твёрдой земной поверхности и иных твёрдых планетных тел, разнообразных по очертаниям, размерам, происхождению, возрасту и истории развития.
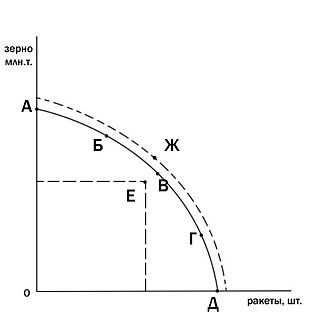
Крива́я произво́дственных возмо́жностей — это кривая, показывающая различные комбинации максимальных объёмов производства нескольких благ, которые могут быть созданы в условиях полной занятости при использовании всех имеющихся в экономике ресурсов
Неприятие риска — понятие в экономике, финансах и в психологии, характеризующее склонность потребителей и инвесторов к принятию того или иного решения в условиях риска. О неприятии риска говорят, когда инвестор предпочитает определённый результат неопределенному результату с тем же средним доходом. Например, не приемлющий риск инвестор скорее положит свои деньги на банковский счет с низкой, но гарантированной процентной ставкой вместо того, чтобы вложиться в акции, в среднем обеспечивающие более высокую доходность, но при этом несущие высокий риск потери части инвестиций.

Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. Является точкой равновесия в чистых стратегиях. В такой точке, если рассматривается функция двух переменных, образованная графиком функции поверхность обычно напоминает по форме седло или горный перевал — выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний. Например, два холма, между которыми находится высокий перевал, образуют седловую точку в вершине этого перевала: на карте высот это будет выглядеть как центр «восьмерки», образованной соответствующими изолиниями.

Тело Кеплера — Пуансо — тело, представляющее собой правильный звёздчатый многогранник, не являющийся соединением платоновых и звёздчатых тел.
Вершина — точка, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников.

Многогранник Шёнхардта — простейший невыпуклый многогранник, который нельзя триангулировать тетраэдрами без добавления новых вершин. Многогранник назван именем немецкого математика Эриха Шёнхардта, построившего его в 1928 году.

Лестница Шрёдера представляет собой оптическую иллюзию, а именно двухмерный рисунок, который можно восприниматься либо как рисунок лестницы, ведущей слева направо вниз, либо той же самой лестницы, только перевёрнутой вверх дном. Это классический пример изменения перспективы в психологии восприятия. Она названа в честь немецкого естествоиспытателя Генриха Г. Ф. Шрёдера, который опубликовал её в 1858 году.
















