В физике, Уравнения Эйлера описывают вращение твердого тела в системе координат, связанной с самим телом.
Колесо́ — движитель, свободно вращающийся или закреплённый на вращающейся оси диск, позволяющий поставленному на него телу катиться, а не скользить.
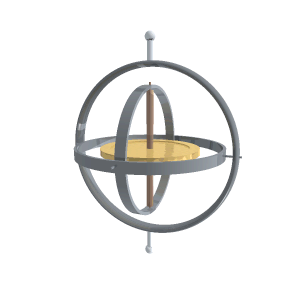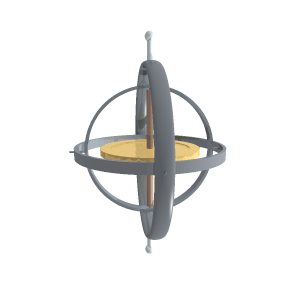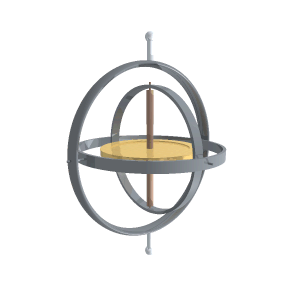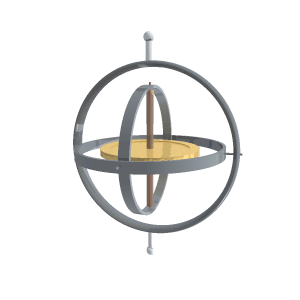
Гироско́п — устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено, относительно инерциальной системы отсчёта. Простейший пример гироскопа — юла (волчок).
Си́ла Кориоли́са — одна из сил инерции, использующаяся при рассмотрении движения материальной точки относительно вращающейся системы отсчёта. Добавление силы Кориолиса к действующим на материальную точку физическим силам позволяет учесть влияние вращения системы отсчёта на такое движение.
Преце́ссия — явление, при котором ось вращения тела меняет своё направление в пространстве.
Подши́пник — сборочный узел, являющийся частью опоры или упора и поддерживающий вал, ось или иную подвижную конструкцию с заданной жёсткостью. Фиксирует положение в пространстве, обеспечивает вращение, качение с наименьшим сопротивлением, воспринимает и передаёт нагрузку от подвижного узла на другие части конструкции.
Существует множество математических и физических объектов, названных в честь Леонарда Эйлера, что породило шуточное фольклорное правило: «В математике принято называть открытие именем второго человека, который его сделал — иначе пришлось бы всё называть именем Эйлера».
Групповая скорость — это величина, характеризующая скорость распространения «группы волн» — то есть более или менее хорошо локализованной квазимонохроматической волны. Обычно интерпретируется как скорость перемещения максимума амплитудной огибающей квазимонохроматического волнового пакета. В случае рассмотрения распространения волн в пространстве размерностью больше единицы подразумевается, как правило, волновой пакет, близкий по форме к плоской волне.
Маховик — массивное вращающееся колесо, использующееся в качестве накопителя кинетической энергии или для создания инерционного момента, как это используется на космических аппаратах.
Гироскопический тренажёр — малогабаритный спортивный тренажёр, принцип работы которого основан на свойствах роторного гироскопа. Используется для создания нагрузки мышц и суставов кисти руки. Для достижения высоких степеней раскручивания ротора гироскопического тренажёра задействуются мышцы предплечья, плеча и плечевого пояса.
Со́лнечно-синхро́нная орби́та — геоцентрическая орбита с такими параметрами, что объект, находящийся на ней, проходит над любой точкой земной поверхности приблизительно в одно и то же местное солнечное время. Таким образом, угол освещения земной поверхности будет приблизительно одинаковым на всех проходах спутника. Такие постоянные условия освещения очень хорошо подходят для спутников, получающих изображения земной поверхности. Однако присутствуют годовые колебания солнечного времени, вызванные эллиптичностью земной орбиты.
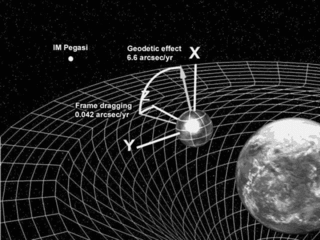
Увлече́ние инерциа́льных систе́м отсчёта, или эффе́кт Ле́нзе — Ти́рринга, — явление в общей теории относительности (ОТО), наблюдаемое вблизи вращающихся массивных тел. Эффект проявляется в появлении дополнительных ускорений, сходных с ускорением Кориолиса, то есть, в итоге, сил, действующих на пробные тела, двигающиеся в гравитационном поле.
Кинема́тика твёрдого тела — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины. В силу относительности движения, обязательно указание системы отсчёта, относительно которой описывается движение.
Число Тейлора (Ta) — два сходных критерия подобия в гидродинамике.
Преце́ссия То́маса — кинематический эффект специальной теории относительности, проявляющийся в изменении ориентации векторов, связанных с неинерциальной системой отсчёта, относительно лабораторной системы отсчёта. Использован Люэлином Томасом в 1926 году для объяснения спин-орбитального взаимодействия электрона в атоме. Если на вращающийся гироскоп действует сила, изменяющая его скорость, но отсутствует момент силы, то в классической механике такой гироскоп при движении будет сохранять ориентацию собственного момента вращения (спина). В теории относительности это уже не так, и при изменении скорости гироскопа будет происходить и изменение вектора его спина. Математически этот эффект связан с групповыми свойствами преобразований Лоренца — их некоммутативностью.
Уравне́ние ви́хря — дифференциальное уравнение в частных производных, описывающее эволюцию в пространстве и времени вихря скорости течения жидкости или газа. Под вихрем скорости (завихренностью) понимается ротор скорости 
. Уравнение вихря используется в гидродинамике, геофизической гидродинамике, астрофизической гидродинамике, в численном прогнозе погоды.
Тео́рия во́лн пло́тности — теория, предложенная Цзяцяо Линем и Фрэнком Шу в середине 1960-х гг. для объяснения спиральной структуры спиральных галактик. Она основана на идее о долгоживущих квазистационарных волнах плотности, представляющих собой участки диска галактики, обладающие повышенной плотностью. Эта теория также была успешно применена к системе колец Сатурна.
Прецессия линии узлов — прецессия орбитальной плоскости спутника вокруг оси вращения астрономического объекта. Такой вид прецессии возникает из-за несферичности вращающегося тела, создающей неизотропное гравитационное поле. Следующие рассуждения относятся к спутникам на низкой околоземной орбите, не оказывающим заметного влияния на движение Земли. Прецессия линии узлов более массивных естественных спутников, например, Луны, более сложна.
Экваториальное утолщение, экваториальный балдж — различие между экваториальным и полярным диаметрами планеты, возникающее вследствие центробежной силы, вызванной вращением вокруг оси тела. Вращающееся тело стремится к формированию сжатого сфероида, а не шара.
