Кардиоида


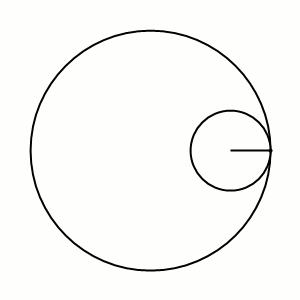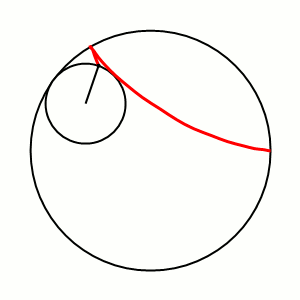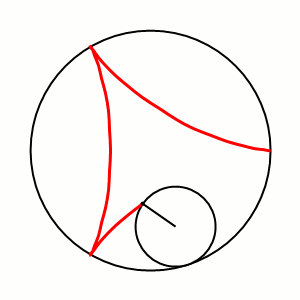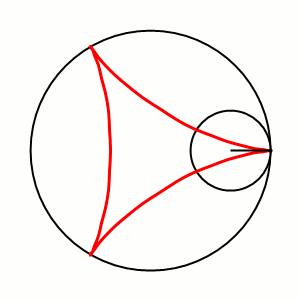
Кардио́ида, или сердцеви́дная крива́я[1] (греч. καρδία — сердце, греч. εἶδος — вид) — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом[2]. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.
Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали, а также подерой окружности с полюсом на этой окружности, антиподерой секстики Кэли[англ.] и инверсией параболы.
Уравнения

Пусть — радиусы окружностей, начало координат находится в крайней правой или левой точке горизонтального диаметра неподвижной окружности (см. рисунок). Тогда уравнения кардиоиды можно записать в следующих формах[3]:
В прямоугольных координатах с началом координат в центре неподвижной окружности (параметрическая запись):
то же самое на комплексной плоскости (параметрическая запись)[4]:
Во всех уравнениях этого раздела в знаках и верхний знак соответствует началу координат и каспу справа, нижний — слева.
Свойства
- Кардиоида является частным случаем улитки Паскаля
- Кардиоида является частным случаем синусоидальной спирали
- Кардиоида — алгебраическая кривая четвёртого порядка.
- Кардиоида имеет один касп.
- Кардиоида — подера окружности с полюсом на этой окружности — каспе кардиоиды.
- Длина дуги одного витка кардиоиды, заданной формулой в полярных координатах
- равна:
- Площадь фигуры, ограниченной кардиоидой, заданной формулой в полярных координатах
- равна:
- .
Радиус кривизны любой линии:
Что даёт для кардиоиды заданной уравнением в полярных координатах:
Обобщение

- Кардиоида есть Синусоидальная спираль при ;
- Кардиоида есть Улитка Паскаля при .

История
Кардиоида впервые встречается в трудах французского учёного Луи Карре (Louis Carrè, 1705 г.). Название кривой дал в 1741 году Джованни Сальвемини ди Кастиллоне (он упоминается также как Johann Francesco Melchiore Salvemini Castillon).
«Спрямление», то есть вычисление длины кривой, выполнил Ла Ир (Philippe de La Hire), который открыл кривую независимо, в 1708 году. Также независимо описал кардиоиду голландский математик Й. Коерсма (J. Koersma, 1741 год). В дальнейшем к кривой проявляли интерес многие видные математики XVIII—XIX веков.
Микрофоны
Односторонняя направленность достигается в микрофонах комбинированного типа. Их диаграммы направленности близки по форме к кардиоиде, поэтому нередко их называют кардиоидными. Модификации микрофонов, имеющих ещё меньшую направленность, чем кардиоидные, называют суперкардиоидными и гиперкардиоидными, однако эти разновидности, в отличие от кардиоидного микрофона, также чувствительны к сигналам с противоположной стороны.
Эти микрофоны имеют определённые преимущества в эксплуатации: источник звука располагается с одной стороны микрофона в пределах достаточно широкого пространственного угла, а звуки, распространяющиеся за его пределами, микрофон не воспринимает[5].
См. также
Примечания
- ↑ Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве, 1997, § 2. Атлас кривых. Кардиоида (сердцевидная кривая), с. 93.
- ↑ 1 2 3 Энциклопедический словарь юного математика, 1985.
- ↑ 1 2 Савелов А. А., 1960, с. 121—122.
- ↑ Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XX. Cardioid and limaçon, p. 257.
- ↑ КАРДИОИДНЫЙ МИКРОФОН - ОПИСАНИЕ, ОСОБЕННОСТИ, СФЕРА ПРИМЕНЕНИЯ. Дата обращения: 6 апреля 2024. Архивировано 6 апреля 2024 года.
Литература
- Савелов А. А. Плоские кривые: Систематика, свойства, применения (справочное руководство). — М.: Физматлит, 1960. — С. 230—233. — 293 с.. Переиздана в 2002 году, ISBN 5-93972-125-7.
- Кардиоида // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 130—131. — 352 с.
- Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве. Справочник с приложенипем дискеты «Плоские кривые». М.: ФАЗИС, 1997. 334 с., ил. ISBN 5-7036-0027-8.
- Zwikker C.[англ.] The Advanced Geometry of Plane Curves and Their Applications[англ.]The Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 0486610780. ISBN 9780486610788.











![{\displaystyle \rho (\varphi )={\frac {\left[r(\varphi )^{2}+{\dot {r}}(\varphi )^{2}\right]^{3/2}}{r(\varphi )^{2}+2{\dot {r}}(\varphi )^{2}-r(\varphi ){\ddot {r}}(\varphi )}}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e7cf0dc8bbc7c290a5046d1002a3ad215646126)

![{\displaystyle \rho (\varphi )=\cdots ={\frac {[16a^{2}\sin ^{2}{\frac {\varphi }{2}}]^{\frac {3}{2}}}{24a^{2}\sin ^{2}{\frac {\varphi }{2}}}}={\frac {8}{3}}a\sin {\frac {\varphi }{2}}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96bb1da147c75324fa46d5269285eff17ce395a)