
Ква́нтовая тео́рия по́ля (КТП) — раздел физики, изучающий поведение квантовых систем с бесконечно большим числом степеней свободы — квантовых полей; является теоретической основой описания микрочастиц, их взаимодействий и превращений. На языке КТП основываются физика высоких энергий и физика элементарных частиц, её математический аппарат используется в физике конденсированного состояния. КТП в виде Стандартной модели в настоящее время является единственной экспериментально подтверждённой теорией, способной описывать и предсказывать результаты экспериментов при достижимых в современных ускорителях высоких энергиях.

Ква́нтовая гравита́ция — направление исследований в теоретической физике, целью которого является квантовое описание гравитационного взаимодействия.
В физике квантова́ние — построение квантового варианта некоторой неквантовой (классической) теории или физической модели в соответствии с аксиомами квантовой физики.

Ю́рий Ива́нович Ма́нин — советский, впоследствии русско-немецкий математик, алгебраический геометр, педагог. Один из основоположников некоммутативной алгебраической геометрии, теории квантовых вычислений и квантовой информатики.
При́нцип соотве́тствия в методологии науки — утверждение, что любая новая научная теория должна включать старую теорию и ее результаты как частный случай. Например, закон Бойля — Мариотта является частным случаем уравнения состояния идеального газа в приближении постоянной температуры; кислоты и основания Аррениуса являются частным случаем кислот и оснований Льюиса и т. п.

Лю́двиг Дми́триевич Фадде́ев — советский и российский физик-теоретик и математик, специалист в области математической физики, действительный член Академии наук СССР (1976), позднее Российской академии наук. Почётный гражданин Санкт-Петербурга (2010). Президент Международного математического союза (1987—1990).
Влади́мир Ге́ршонович Дри́нфельд — советский, украинский и американский математик. Заслуженный профессор Чикагского университета, член НАН США (2016), член-корреспондент НАН Украины (1992), иностранный член Французской АН. Лауреат Филдсовской премии (1990) и премии Вольфа по математике.
Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число.
Квантовый вихрь — топологический дефект, который проявляется в сверхтекучей жидкости и сверхпроводниках. Квантование циркуляции скорости в сверхпроводящих жидкостях отличается[чем?] от квантования в сверхпроводниках, но сохраняется ключевое подобие, которое состоит в топологичности дефектов, а также в том, что они квантуются.
Квантовая вероятность — некоммутативный аналог классической (колмогоровской) теории вероятности и теории стохастических процессов.
Некоммутативным случайным процессом называется случайный процесс над C*-алгеброй B с множеством значений параметра  как совокупность из C*-алгебры A, семейства
как совокупность из C*-алгебры A, семейства  гомоморфизмов алгебры B в A и состояния
гомоморфизмов алгебры B в A и состояния  на A.
на A.
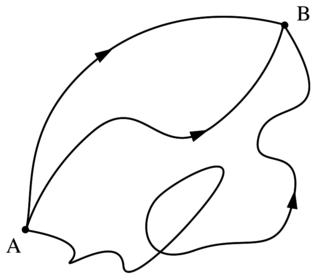
Формулировка квантовой механики через интеграл по траекториям — описание квантовой теории, которое обобщает принцип действия классической механики. Оно замещает классическое определение одиночной, уникальной траектории системы полной суммой по бесконечному множеству всевозможных траекторий для расчёта квантовой амплитуды. Методологически формулировка через интеграл по траекториям близка к принципу Гюйгенса — Френеля из классической теории волн.
Универсальная обёртывающая алгебра — ассоциативная алгебра, которая может быть построена для любой алгебры Ли, перенимающая многие важные свойства исходной алгебры, что позволяет применить более широкие средства для изучения исходной алгебры.
Уравнение Янга — Бакстера — уравнение, относящееся к классу точно решаемых задач. Имеет вид локальных преобразований эквивалентности, которые появляются в самых разнообразных случаях, таких как электрические цепи, теория узлов и теория кос, спиновые системы. Получило своё имя от независимых работ Ч. Н. Янга 1968 г. и Р. Д. Бакстера 1971 г. по статистической механике.
Алгебра Хопфа — ассоциативная алгебра над полем, имеющая единицу и являющаяся также коассоциативной коалгеброй с коединицей c антигомоморфизмом специального вида. Названа в честь Хайнца Хопфа.
Ста́рая ква́нтовая тео́рия — подход к описанию атомных явлений, который был развит в 1900—1924 годах и предшествовал созданию квантовой механики. Характерная черта этой теории — одновременное использование классической механики и некоторых предположений, вступавших в противоречие с ней. Основа старой квантовой теории — модель атома Бора, к которой позднее Арнольд Зоммерфельд добавил квантование z-компоненты углового момента, неудачно названное пространственным квантованием. Квантование z-компоненты дало возможность ввести эллиптические электронные орбиты и предложить концепцию энергетического вырождения. Успех старой квантовой теории состоял в корректном описании атома водорода и нормального эффекта Зеемана.
Квантовый дилогарифм — это специальная функция, определяемая формулой

Леон Арменович Тахтаджян — российский, советский, армянский физик, математик, профессор математики Университета в Стоуни-Брук и ведущий научный сотрудник Международного математического института им. Л. Эйлера в Санкт-Петербурге.
В представлении фазового пространства квантовая механика трактует единообразно как координаты, так и импульсы частиц, которые образуют фазовое пространство, в отличие от трактовки Шредингера, где используется координатное или импульсное представления. Два ключевых элемента физической картины в представлении фазового пространства состоят в следующем: квантовое состояние описывается квазивероятностным распределением, и оператор умножения заменяется звёздочным произведением.
В квантовой механике, преобразование Вигнера — Вейля — обратимое отображение функций в представлении фазового пространства на операторы гильбертова пространства в представлении Шредингера.
Игорь Викторович Широков — советский и российский учёный, специалист в области теоретической и математической физики, криптографии, доктор физико-математических наук, профессор.


![{\displaystyle k[G_{q}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de82ca82ae4f86b2df44d86624cb582bec6c01ab)









