Кривая Циндлера

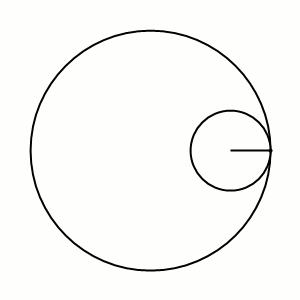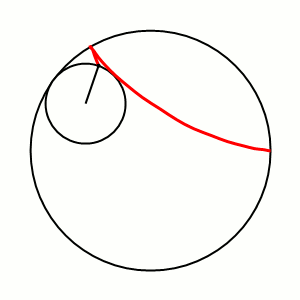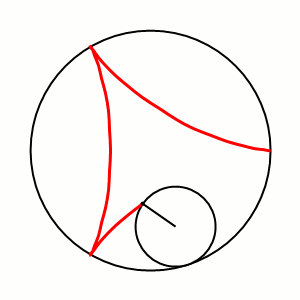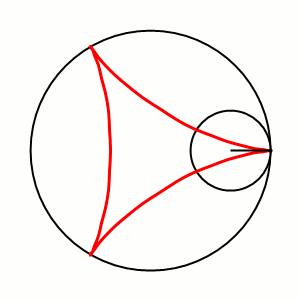
Кривая Циндлера — простая замкнутая плоская кривая, у которой все хорды, делящие её длину пополам, имеют равные длины. Эквивалентное определение — простая замкнутая плоская кривая, все хорды которой, делящие ограниченную ей площадь фигуры пополам, имеют равные длины. Простейший пример такой кривой — окружность.
Впервые в такой общности исследованы австрийским математиком Конрадом Циндлером[нем.]; дальнейшие результаты получил Герман Ауэрбах в 1938 году, он же впервые назвал класс кривых именем Циндлера. В частности Ауэрбах доказал, что объект, ограниченный кривой Циндлера, обладающий половиной плотности воды, будет плавать в воде в любом положении. Это даёт отрицательный ответ на двумерную версию задачи Станислава Улама о плавающих телах (задача 19 из Шотландской книги), в которой задаётся вопрос, является ли диск единственной фигурой однородной плотности, которая будет плавать в воде в любом положении[1].
Кривые Циндлера также связаны с задачей о том, возможно ли определить направление движения велосипеда, учитывая только замкнутые заднюю и переднюю колеи[2].

Пример — любая из кривых с вещественным параметром :
является кривой Циндлера[3]. При такая кривая выпукла. Для эти кривые имеют отношение к кривым постоянной ширины[].
Примечания
- ↑ В исходной задаче спрашивается, является ли сфера единственным твёрдым телом, обладающим тем же свойством в трёхмерном пространстве.
- ↑ Bor, Gil; Levi, Mark; Perline, Ron; Tabachnikov, Sergei (2018). "Tire Tracks and Integrable Curve Evolution". International Mathematics Research Notices (англ.). 2020 (9): 2698—2768. doi:10.1093/imrn/rny087.
- ↑ W. Wunderlich: Algebraische Beispiele ebener und räumlicher Zindler-Kurven. Publ. Math. Debrecen 24 (1977), 289—297.(S. 291).
Ссылки
- Herman Auerbach: Sur un problème de M. Ulam concernant l’équilibre des corps flottants (PDF; 796 kB), Studia Mathematica 7 (1938), 121—142.
- K. L. Mampel: Über Zindlerkurven, Journal für reine und angewandte Mathematik 234 (1969), 12-44.
- Konrad Zindler: Über konvexe Gebilde. II. Teil, Monatshefte für Mathematik und Physik 31 (1921), 25-56.
- H. Martini, S. Wu: On Zindler Curves in Normed Planes, Canadian Mathematical Bulletin 55 (2012), 767—773.
- J. Bracho, L. Montejano, D. Oliveros: Carousels, Zindler curves and the floating body problem, Periodica Mathematica Hungarica 49 (2004), 9-23.
- P. M. Gruber, J.M. Wills: Convexity and Its Applications, Springer, 1983, ISBN 978-3-0348-5860-1, p. 58.




![{\displaystyle z(u)=x(u)+iy(u)=e^{2iu}+2e^{-iu}+ae^{iu/2}\;,\ u\in [0;4\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc7690de80d79d6994203b2ef852792ba6a7f857)