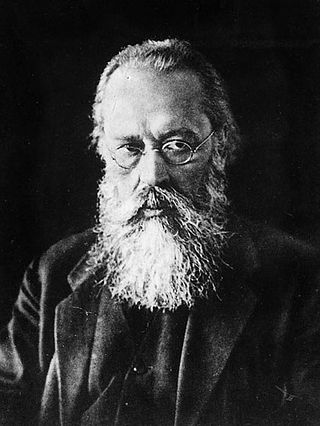Матиясевич, Юрий Владимирович

Юрий Владимирович Матиясевич
Во время проведения JASS 08
Имя при рождении	Юрий Владимирович Матиясевич
Дата рождения	2 марта 1947(1947-03-02) (77 лет)
Место рождения	Ленинград, РСФСР, СССР
Страна	СССР  Россия
Род деятельности	математик, специалист в области информатики, преподаватель университета
Научная сфера	теоретическая информатика
Место работы	ПОМИ
Альма-матер	ЛГУ (матмех)
Учёная степень	доктор физико-математических наук
Учёное звание	академик РАН (2008)
Научный руководитель	С. Ю. Маслов Н. А. Шанин
Известен как	автор решения десятой проблемы Гильберта
Награды и премии	премия Маркова (1980), премия Гумбольдта (1998)
Сайт	logic.pdmi.ras.ru/~yumat/
Медиафайлы на Викискладе

Ю́рий Влади́мирович Матиясе́вич (род. 2 марта 1947, Ленинград) — советский и российский математик, исследователь Санкт-Петербургского отделения Математического института им. В. А. Стеклова РАН, член экспертной комиссии РСОШ по математике, академик Российской академии наук, доктор физико-математических наук. Внёс существенный вклад в теорию вычислимости, завершив решение десятой проблемы Гильберта.

Юрий Матиясевич родился в Ленинграде 2 марта 1947 года. Первые несколько классов учился в школе № 255 у Софьи Григорьевны Генерсон, благодаря которой заинтересовался математикой. С 1961 года начал принимать участие во всероссийских олимпиадах. В 1962—1963 годах учился в физико-математической школе № 239 Ленинграда. Также с 7 по 9 класс занимался в математическом кружке Ленинградского дворца пионеров. В 1963—1964 годах закончил 10-й класс в московской физико-математической школе-интернате № 18 при МГУ^[1][2].

В 1964 году стал победителем Международной олимпиады, после чего без экзаменов зачислен на математико-механического факультета Ленинградского университета, где проучился до 1969 года. Экзамены на аттестат зрелости (о среднем образовании) сдавал уже студентом первого курса^[1][3].

В 1966 году, на втором курсе университета, выполнил две работы по математической логике, напечатанные затем в «Докладах Академии наук СССР», и по ним сделал доклад на Международном математическом конгрессе, проходившем в Москве^[2].

По окончании университета поступил в аспирантуру Ленинградского отделения Института имени Стеклова (ЛОМИ), в 1970 году под руководством Сергея Юрьевича Маслова защитил диссертацию на соискание степени кандидата физико-математических наук. Будучи аспирантом, решил десятую проблему Гильберта➤^[4].

В 1972 году в возрасте 25 лет защитил докторскую диссертацию по неразрешимости 10-й проблемы Гильберта^[5].

С 1974 года Матиясевич работал на научных должностях в ЛОМИ: сначала старшим научным сотрудником, а в 1980 году возглавил лабораторию математической логики. В 1995 году Матиясевич стал профессором Санкт-Петербургского университета на кафедре математического обеспечения ЭВМ, впоследствии — на кафедре алгебры^[6].

В 1997 году избран членом-корреспондентом РАН^[6].

С 1998 года — вице-президент Санкт-Петербургского математического общества^[7].

С 2002 года — председатель жюри Санкт-Петербургской городской математической олимпиады. С 2003 года — соруководитель ежегодной русско-немецкой студенческой школы JASS^[8].

В 2008 году избран действительным членом Российской академии наук^[9]. В том же году избран президентом Санкт-Петербургского математического общества.

Матиясевич входит в редколлегию журнала «Записки научных семинаров ПОМИ», а также редсоветы журналов «Дискретная математика» и «Компьютерные инструменты в образовании». Член Американского математического общества и Ассоциации символьной логики. Как педагог, Матиясевич подготовил 2 докторов наук и 3 кандидатов^[10].

Дочь — Дарья Русакова (род. 1979), математик, педагог, игрок спортивного «Что? Где? Когда?»^[].

Матиясевич является автором свыше 100 научных публикаций, среди которых — монография «Десятая проблема Гильберта»^[10].

• Будучи аспирантом, в начале 1970 года в возрасте 22 лет сделал последний шаг в доказательстве алгоритмической неразрешимости задачи о существовании решений у произвольного диофантова уравнения, известной также как десятая проблема Гильберта, завершив тем самым программу исследований, основную часть которой к тому времени выполнили Мартин Дэвис, Хилари Патнем и Джулия Робинсон. Вклад Матиясевича в решение проблемы заключается в том, что он предъявил 10 диофантовых уравнений первой и второй степени, которые задают условие ${\displaystyle b=F_{2a}}$, где через ${\displaystyle F_{n}}$ обозначено ${\displaystyle n}$-е число Фибоначчи^[11].

• Теория чисел: Матиясевич получил ответ на поставленный в 1927 году вопрос Дьёрдя Пойи, касающийся бесконечной системы неравенств, связывающих тейлоровские коэффициенты ${\displaystyle \xi }$-функции Римана: показал, что все эти неравенства являются следствием одного функционального неравенства, связывающего фурье-преобразование ${\displaystyle \xi }$-функции и его производные^[12].

• Теория графов: предложил несколько критериев раскрашиваемости графов, установил неожиданную связь проблемы четырёх красок и делимости биномиальных коэффициентов, дал вероятностную интерпретацию теоремы о четырёх красках^[12].

• Обнаружил ряд новых интересных свойств нулей дзета-функции Римана^[10].

• 1964 — в составе команды советских школьников завоевал диплом первой степени на Международной математической олимпиаде, проходившей в Москве^[13].
• 1970 — премия «Молодому математику» Ленинградского математического общества^[14].
• 1980 — премия имени А. А. Маркова Академии наук СССР.
• 1996 — звание почётного доктора Университета Оверни.
• 1998 — лауреат премии Гумбольдта.
• 2003 — звание почётного доктора Университета Париж-VI^[6].

Автор книги о десятой проблеме Гильберта и большого количества статей в научных журналах, в том числе совместно с Джулией Робинсон, Ричардом Гаем (благодаря последнему персональное число Эрдёша — 2).

• Матиясевич Ю. В. Десятая проблема Гильберта — М.: Наука, 1993.

• Ю. В. Матиясевич. Распознавание в реальное время отношения вхождения // Записки семинаров Ленинградского отделения Математического института им. В. А. Стеклова Академии Наук СССР. — 1971. — Т. 20. — С. 104—114.
• Yuri Matiyasevich and Julia Robinson, Reduction of an arbitrary Diophantine equation to one in 13 unknowns, Acta Arithmetica, XXVII (1975), 521—549.
• Yuri Matiyasevich and Géraud Senizerguez, Decision Problems for Semi-Thue Systems with a Few Rules, LICS’96.
• Yuri Matiyasevich, Proof Procedures as Bases for Metamathematical Proofs in Discrete Mathematics, Personal Journal of Yury Matiyasevich.
• Yuri Matiyasevich, Elimination of bounded universal quantifiers standing in front of a quantifier-free arithmetical formula, Personal Journal of Yuri Matiyasevich.
• Yuri Matiyasevich, One Probabilistic Equivalent of the Four Color Conjecture, Теория вероятности и её применения, 48 (2003), 411—416.
• Статьи Ю. В. Матиясевича в журнале «Квант» (1971—1978)

• Бельтюков А. П. К юбилею Юрия Владимирович Матиясевича // Компьютерные инструменты в образовании. — 2017. — № 6.
• Варпаховский Ф., Колмогоров А. О решении десятой проблемы Гильберт // «Квант». — 1970. — № 7. — С. 38—44.

• Yuri Matiyasevich’s home page.
• Профиль Ю. В. Матиясевича на официальном сайте РАН

• История решения Десятой проблемы Гильберта  (неопр.). Дата обращения: 5 марта 2007. Архивировано из оригинала 16 декабря 2010 года.
• Matiyasevich theorem on Scholarpedia (англ.).
• Yuri Matiyasevich at DBLP (англ.).