Метри́ческое простра́нство — множество вместе со способом измерения расстояния между его элементами. Является центральным понятием геометрии и топологии.
Теорема Хопфа — Ринова — теорема дифференциальной геометрии, доказанная Хайнцем Хопфом и его учеником Вилли Риновым. Опубликована последним в 1931 году.
Внутренняя метрика — метрика в пространстве, определяемая с помощью функционала длины, как инфимум длин всех путей (кривых), соединяющих данную пару точек.
Изгибаемый многогранник — многогранник, чью пространственную форму можно изменить непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров, а деформация осуществляется только за счёт непрерывного изменения двугранных углов. Такая деформация называется непрерывным изгибанием многогранника.
Обобщённая задача коммивояжёра — задача комбинаторной оптимизации, являющаяся обобщением хорошо известной задачи коммивояжёра. Исходными данными для задачи является множество вершин, разбиение этого множества на так называемые кластеры, а также матрица стоимостей перехода из одной вершины в другую. Задача заключается в нахождении кратчайшего замкнутого пути, который бы посетил по одной вершине в каждом кластере.
Метрика Громова — Хаусдорфа — способ определить расстояние между двумя компактными метрическими пространствами. Более точно, это метрика на множестве изометрических классов компактных метрических пространств.
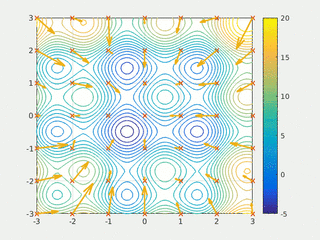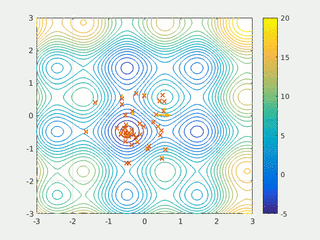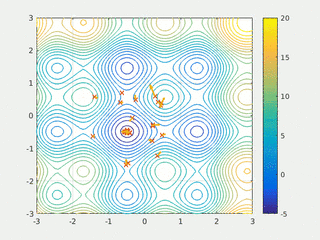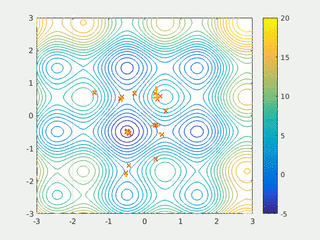
Метод роя частиц (МРЧ) — метод численной оптимизации, для использования которого не требуется знать точного градиента оптимизируемой функции.
Неравенство Безиковича в дифференциальной геометрии — соотношение, которое даёт нижнюю оценку площади поверхности с краем, допускающей параметризацию квадратом 
. Названо по имени Абрама Безиковича.
Сергей Владимирович Иванов — российский математик, доктор физико-математических наук, член-корреспондент Российской академии наук по отделению математических наук; избран 22 декабря 2011 года. Основные работы относятся к дифференциальной и метрической геометрии.
Задача Нелсона — Эрдёша — Хадвигера — задача комбинаторной геометрии, первоначально поставленная как задача о раскраске или хроматическом числе евклидова пространства.
Гипотеза Эрдёша о числе различных расстояний — утверждение комбинаторной геометрии, согласно которому между 
различными точками на плоскости имеется не меньше, чем 
различных расстояний. Гипотеза сформулирована Палом Эрдёшем в 1946 году, в 2010 году Ларри Гут и Нетс Катц объявили о возможном решении этой проблемы, окончательное доказательство Гута и Каца было завершено в 2015 году.
Алгоритм Кармаркара — это алгоритм, представленный Нарендрой Кармаркаром в 1984 году для решения задач линейного программирования. Это был первый достаточно эффективный алгоритм, который решал задачи за полиномиальное время. Метод эллипсоидов является также алгоритмом полиномиального времени, но он оказался неэффективным в практических приложениях.
Задача о триангуляции многоугольника — классическая задача комбинаторной и вычислительной геометрии, состоящая в нахождении триангуляции многоугольника без дополнительных вершин.
Задача о размещении объектов, известная также как анализ расположения оборудования или задача k-центра, — это ветвь исследования операций и вычислительной геометрии, исследующей оптимальное расположение объектов с целью минимизировать цены перевозок с учётом таких ограничений, как размещение опасных материалов вблизи жилищ. Техника применима также к кластерному анализу.
Александровская геометрия — своеобразное развитие аксиоматического подхода в современной геометрии. Идея состоит в замене определённого равенства в аксиоматике евклидова пространства на неравенство.
Геометрический центр дискретного множества точек евклидова пространства — это точка, в которой минимизируется сумма расстояний до точек множества. Геометрический центр обобщает медиану в математической статистике, которая минимизирует расстояния в одномерной выборке данных. Таким образом, геометрический центр отражает центральную тенденцию в пространствах высокой размерности. Понятие известно также по названиям 1-медиана, пространственная медиана, или точка Торричелли.
Рубе́н Ви́кторович Амбарцумя́н — советский и армянский математик. Академик Национальной академии наук Республики Армения, доктор физико-математических наук (1975), профессор (1976). Автор серии работ по стохастической и интегральной геометрии.
Управляемый локальный поиск — это метаэвристический метод поиска, то есть метод поверх алгоритма локального поиска с целью изменить его поведение.
Алексей Августинович Тужилин — российский математик, доктор физико-математических наук (1997), профессор (2019) кафедры дифференциальной геометрии и приложений механико-математического факультета МГУ.
