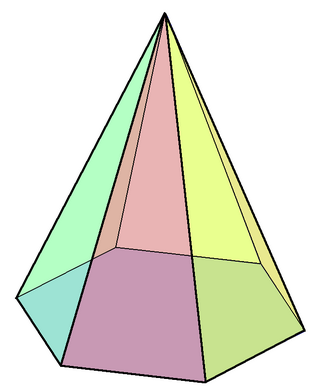
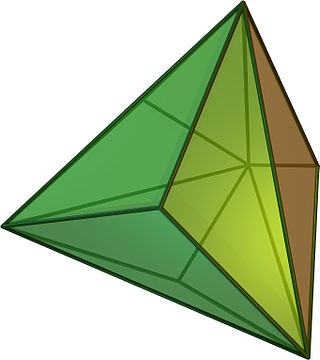
Правильный многогранник или плато́ново тело — это выпуклый многогранник, грани которого являются равными правильными многоугольниками, обладающий пространственной симметрией следующего типа: все многогранные углы при его вершинах правильные и равны друг другу.

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как
 ,
,

Пра́вильный икоса́эдр — правильный выпуклый многогранник, двадцатигранник, одно из платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.

Тетра́эдр — простейший многогранник, гранями которого являются четыре треугольника.

Окта́эдр — многогранник с восемью гранями.

Куб ; иногда гекса́эдр или правильный гекса́эдр — многогранник, поверхность которого состоит из шести квадратов. Куб является правильным многогранником. Частный случай параллелепипеда и призмы.

Параллелепи́пед — четырёхугольная призма, все грани которой являются параллелограммами.

Ромбоэдр — это геометрическое тело, являющееся обобщением куба, у которого грани не обязательно квадратны, а лишь являются ромбами. Ромбоэдр является параллелепипедом, в котором все рёбра равны. Ромбоэдр можно использовать для определения ромбоэдрической решётчатой системы, сот с ромбоэдрическими ячейками.

Тетраэдр называется правильным, если все его грани — равносторонние треугольники.

Равногранный тетраэдр — определённый тип тетраэдра в евклидовом пространстве.
Соразмерный тетраэдр — тетраэдр, бивысоты которого равны.
Третья проблема Гильберта — третья из проблем, поставленных Давидом Гильбертом в его знаменитом докладе на II Международном Конгрессе математиков в Париже в 1900 году. Эта проблема посвящена вопросам равносоставленности многогранников: возможности разрезания двух многогранников равного объёма на конечное число равных частей-многогранников.

Наращённый усечённый тетра́эдр — один из многогранников Джонсона.

Удлинённый трёхска́тный прямо́й бику́пол — один из многогранников Джонсона.
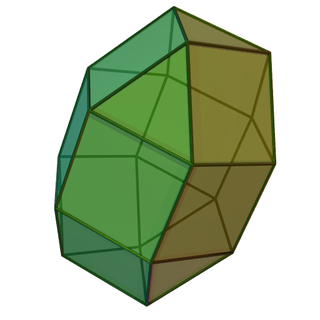
Удлинённый трёхска́тный повёрнутый бику́пол — один из многогранников Джонсона.

Удлинённый трёхска́тный ку́пол — один из многогранников Джонсона.