
Геоме́трия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. В практических задачах геометрия позволяет предсказывать геометрические размеры тела, зная другие геометрические размеры этого тела с помощью известных геометрических законов.

Теорема Чевы — классическая теорема аффинной геометрии и геометрии треугольника. Установлена в 1678 году итальянским инженером Джованни Чевой.

Аффи́нное преобразование, иногда афинное преобразование — отображение плоскости или пространства в себя, при котором параллельные прямые переходят в параллельные прямые, пересекающиеся — в пересекающиеся, скрещивающиеся — в скрещивающиеся.
Аффи́нная геоме́трия — раздел геометрии, в котором изучаются свойства фигур, инвариантные относительно аффинных преобразований . Группа аффинных преобразований содержит различные подгруппы, которым соответствуют геометрии, подчинённые аффинной: эквиаффинная геометрия, центроаффинная геометрия и другие.
Аффи́нное простра́нство — математический объект (пространство), обобщающий некоторые свойства евклидовой геометрии. В отличие от векторного пространства, аффинное пространство оперирует с объектами не одного, а двух типов: «векторами» и «точками».

Феликс Христиан Клейн — немецкий математик и педагог. Автор Эрлангенской программы. Внёс значительный вклад в общую алгебру, теорию эллиптических и автоморфных функций.
Репе́р :
- Репер, в геодезии — знак, который находится в определённой точке земной поверхности с известной абсолютной высотой.
- Репер, в геометрии — совокупность точки многообразия и базиса касательного пространства в этой точке.
- Репер или точечный базис аффинного пространства — обобщение понятия базиса для аффинных пространств.
- Репер — действительная или условная точка на местности, используемая для пристрелки артиллерийских орудий.
Евкли́дова геоме́трия — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида. Это геометрия ортогональной группы.

Однородное пространство неформально можно описать, как пространство, в котором все точки одинаковы, то есть существует симметрия пространства, переводящая любую точку в другую. Определение довольно общее и имеет несколько вариантов. Однородное пространство включает в себя пространства классической геометрии, такие как евклидово пространство, пространство Лобачевского, аффинное пространство, проективное пространство и другие.

Алгебраическая геометрия — раздел математики, который объединяет алгебру и геометрию. Главным предметом изучения классической алгебраической геометрии, а также в широком смысле и современной алгебраической геометрии, являются множества решений систем алгебраических уравнений. Современная алгебраическая геометрия во многом основана на методах общей алгебры для решения задач, возникающих в геометрии.
Паралле́льный перено́с, иногда трансляция ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние.
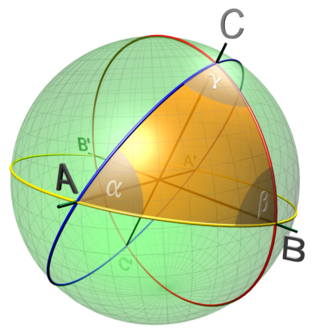
Сферический треугольник — геометрическая фигура на поверхности сферы, состоящая из трёх точек и трёх дуг больших кругов, соединяющих попарно эти точки. Три больших круга на поверхности сферы, не пересекающихся в одной точке, образуют восемь сферических треугольников. Ясно, что стороны сферических треугольников меньше половины большого круга. Соотношения между элементами сферических треугольников изучает сферическая тригонометрия.
Преобразование в математике — отображение (функция) множества в себя. Иногда преобразованиями называют отображения, переводящие некоторое множество в другое множество.

Эрлангенская программа — выступление 23-летнего немецкого математика Феликса Клейна в Эрлангенском университете, в котором он предложил общий алгебраический подход к различным геометрическим теориям и наметил перспективный путь их развития. Доклад был связан с процедурой утверждения Клейна в должности профессора и был опубликован в том же году. Первый русский перевод появился в 1895 году.

Алгебраическое многообразие — центральный объект изучения алгебраической геометрии. Классическое определение алгебраического многообразия — множество решений системы алгебраических уравнений над действительными или комплексными числами. Современные определения обобщают его различными способами, но стараются сохранить геометрическую интуицию, соответствующую этому определению.
Кривизна́:
- Кривизна — отклонение формы объекта от прямой.
- Кривизна ствола — отклонение оси ствола дерева от прямой линии.
Я́ков Петро́вич Пона́рин — советский и российский и советский математик, педагог-математик, автор пособий по элементарной геометрии. Автор учебников по геометрии.




















