Правила Уэйда

Правила Уэйда, англ. Polyhedral skeletal electron pair theory — набор правил подсчета электронов, позволяющих предсказать структуры кластерных соединений, таких как бораны и карбораны. Эти правила впервые были сформулированы Кеннетом Уэйдом (англ. Kenneth Wade) в 1971 году^[1] и затем доработаны Майклом Мингосом (англ. Michael Mingos) и другими исследователями. Правила основаны на представлениях теории молекулярных орбиталей о химической связи^[2]^[3]^[4]^[5].

Предсказание структуры кластерных соединений

Различные правила (4n, 5n или 6n) применяются в зависимости от среднего количества электронов, приходящихся на вершину.

4n правила применимы к структурам, содержащим около 4 электронов на вершину, таким как бораны и карбораны. Основой таких кластеров является дельтаэдр. 4n кластеры подразделяются на клозо-, нидо-, арахно-, гифо- и кладо-, в зависимости числа вершин, недостающих до полноценного дельтаэдра (0 для клозо-, 1 для нидо-, 2 для арахно-, и т. д.).

Однако при избытке электронов, начинают заполняться разрыхляющие молекулярные орбитали, что приводит к дестабилизации кластера, поэтому предпочтительной становится структура, определяемая 5n правилами. Это происходит при увеличении среднего числа электронов на вершину до 5. Основой для 5n структур являются 3-связные многогранники.

Аналогично при дальнейшем увеличении начинают применяться 6n правила. Структура 6n соединений основана на кольцах.

Теория молекулярных орбиталей позволяет более строго разделить 4n, 5n и 6n структуры.

Реальная структура [Re₄(CO)₁₂]²⁻ согласуется с предсказанием правил.

4n правила

Представленные ниже многогранники являются клозо многогранниками и основой для 4n правил^[6]. Количество вершин в кластере определяет, какой из многогранников станет основой структуры кластера.

Количество вершин	Многогранник
4	Тетраэдр
5	Тригональная бипирамида
6	Октаэдр
7	Пентагональная бипирамида
8	Плосконосый двуклиноид
9	Трижды наращённая треугольная призма
10	Скрученно удлинённая четырёхугольная бипирамида
11	Икосаэдр с сжатыми ребрами
12	Икосаэдр

Подсчитывая электроны, можно предсказать структуру вещества. n — количество вершин в кластере. 4n правила приведены в таблице ниже.

Количество электронов	Название	Структура
4n − 2	Двунаращенный клозо	клозо многогранник из n — 2 вершин, 2 грани которого наращены
4n	Наращенный клозо	клозо многогранник из n — 1 вершин, 1 грань которого наращена
4n + 2	клозо	клозо многогранник из n вершин
4n + 4	нидо	клозо многогранник из n+1 вершин, 1 из которых отсутствует
4n + 6	арахно	клозо многогранник из n+2 вершин, 2 из которых отсутствует
4n + 8	гифо	клозо многогранник из n+3 вершин, 3 из которых отсутствует
4n + 10	кладо	клозо многогранник из n+4 вершин, 4 из которых отсутствует

При подсчете общего количества электронов, учитываются только валентные электроны. Для каждого из атомов переходных элементов учитывается на 10 меньше электронов. Например, в Rh₆(CO)₁₆ общее количество электронов будет 6 × 9 + 16 × 2 − 6 × 10 = 86 – 6 × 10 = 26. Геометрия кластера будет представлять клозо многогранник, так как n = 6 и 4n + 2 = 26.

Другие важные правила:

В кластерах состоящих в основном из переходных металлов, любые элементы главных групп, лучше всего рассматривать в качестве лигандов или мостиковых атомов, чем отдельных вершин.
Большие и электроположительные атомы стремятся попасть в вершины с наибольшим числом ребер, в то время как маленькие и электроотрицательные стремятся занять вершины с низким числом ребер.
В частном случае кластеров гидрида бора каждый бор, соединенный с 3 или более вершинами, имеет один концевой водород, а бор, связанный с 2 другими вершинами, имеет 2 концевых водорода. Если присутствует больше атомов водорода, они помещаются в открытые грани, чтобы выровнять координационное число вершин.
Для особого случая кластеров переходных металлов лиганды добавляются к металлическим центрам, чтобы дать металлам разумные координационные числа, и, если присутствуют какие-либо атомы водорода, они помещаются в положения мостиков для выравнивания координационных чисел вершин.

В общем случае клозо структуры представляют собой многогранники с n вершинами.

Чтобы предсказать структуру нидо кластера, необходимо удалить одну вершину из n+1 клозо кластера. То, какая вершина должна быть удалена, определяется свойствами атомов кластера: если они маленькие и электроотрицательные, убирается вершина, принадлежащая наибольшему количеству ребер, если же большие и электроположительные, наоборот.

Чтобы предсказать структуру арахно кластера, необходимо из n + 2 клозо кластера получить соответствующий нидо, используя предыдущее правило. После этого из нидо кластера удаляется вершина, соседняя с удаленной на первом шаге, если атомы маленькие и электроотрицательные, иначе удаляется вершина, не связанная с первой.

Os₆(CO)₁₈, карбонилы не указаны для ясности

Пример: ${\ce {Pb^{2-}10}}$

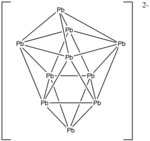
Количество электронов: 10 × Pb + 2 (2- — отрицательный заряд иона) = 10 × 4 + 2 = 42.

Так как n = 10, 4n + 2 = 42, кластер — клозо скрученно удлинённая четырёхугольная бипирамида.

Пример: ${\ce {S^{2+}4}}$

Количество электронов: 4 × S — 2 (2+ — положительный заряд иона) = 4 × 6 — 2 = 22.

Так как n = 4, 4n + 6 = 22, тип кластера — арахно.

Основа структуры — октаэдр (тип — арахно, поэтому основа — n + 2 клозо). Атом серы относительно мал и электроотрицателен, поэтому первой удаляется вершина, принадлежащая наибольшему числу ребер(на самом деле в октаэдре все вершины принадлежат одинаковому количеству ребер). После этого удаляется вершина, не соседняя с предыдущей.

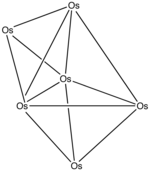
Пример: Os₆(CO)₁₈

Количество электронов: 6 × Os + 18 × CO — 6 × 10(6 атомов осмия, являющегося переходным элементом) = 6 × 8 + 18 × 2 — 60 = 24

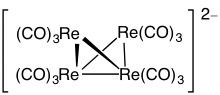
Так как n = 6, 4n = 24, кластер — наращенный клозо.

Основа — тригональная бипирамида. Для получения наращенной клозо структуры, одна из граней наращивается.

Пример: ${\ce {B5H5^{4-}}}$ ^[7]

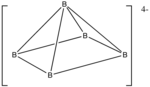
Количество электронов: 5 × B + 5 × H + 4 (-4 — отрицательный заряд иона) = 5 × 3 + 5 × 1 + 4 = 24

Так как n = 5, 4n + 4 = 24, кластер — нидо

Начиная с октаэдра, удаляем одну из вершин.

Правила также полезны при предсказании структур карборанов.

Пример: C₂B₇H₁₃

Количество электронов = 2 × C + 7 × B + 13 × H = 2 × 4 + 3 × 7 + 13 × 1 = 42

Так как n = 9, 4n + 6 = 42, кластер — арахно.

5n правила

При увеличении числа электронов 5n правила начинают лучше предсказывать форму, чем 4n. Основными фигурами являются 3-связные многогранники(в которых каждая из вершин связана с 3 другими).

Количество вершин	3-связного многогранника
4	Тетраэдр
6	Тригональная призма
8	Куб
10	Пентагональная призма
12	Двойственный плосконосому двуклиноиду
14	Усечённая треугольная бипирамида (двойственна тринаращенной треугольной призме)
16	Усечённый четырёхугольный трапецоэдр
18	Двойственный икосаэдру с сжатыми ребрами
20	Додэкаэдр

5n правила

Общее количество электронов	Структура
5n	3-связный многогранник с n вершинами
5n + 1	3-связный многогранник с n-1 вершинами, с 1 вершиной на ребре
5n + 2	3-связный многогранник с n-1 вершинами, с 2 вершинами на ребре
5n + k	3-связный многогранник с n-k вершинами, с k вершинами на ребре

Пример: P₄

Количество электронов: 4 × P = 4 × 5 = 20

Так как n = 4, 5n = 20, кластер — тетраэдр.

Пример: P₄S₃

Количество электронов: 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38

Так как n = 7, 5n + 3 = 38, кластер — тетраэдр с 3 вершинами на ребрах.

Пример: P₄O₆

Количество электронов: 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56

Так как n = 10, 5n + 6 = 56, кластер — тетраэдр с 6 вершинами на ребрах.

6n правила

При увеличении числа электронов в кластере, число электронов на вершину достигает 6. Такие кластеры описываются уже не 4n и 5n правилами, а 6n, которые основаны на кольцах.

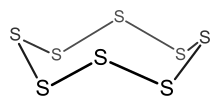
Общее число электронов	Предполагаемая структура
6n — k	n-членное кольцо с k⁄2 трансаннулярными связями
6n — 4	n-членное кольца с 2 трансаннулярными связями
6n — 2	n-членное кольцо с 1 трансаннулярной связью
6n	n-членное кольцо
6n + 2	n-членная цепь (n-членное кольцо с одной разорванной связью)

Пример: S₈

Количество электронов = 8 × S = 8 × 6 = 48.

Так как n = 8, 6n = 48, кластер — восьмичленное кольцо.

6n + 2 кластер: гексан

Пример: Гексан (C₆H₁₄)

Количество электронов = 6 × C + 14 × H = 6 × 4 + 14 × 1 = 38

Так как n = 6, 6n = 36 and 6n + 2 = 38, кластер — 6-членная цепь.

См. также

Теория молекулярных орбиталей

Примечания

↑ Wade, K. The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds : [англ.] // Journal of the Chemical Society D: Chemical Communications. — 1971. — No. 15. — P. 792–793. — doi:10.1039/C29710000792.
↑ Wade, K. Structural and Bonding Patterns in Cluster Chemistry : [англ.] // Advances in Inorganic Chemistry and Radiochemistry. — 1976. — Vol. 18. — P. 1–66. — doi:10.1016/S0065-2792(08)60027-8.
↑ Girolami, G. Lecture notes : These notes contained original material that served as the basis of the sections on the 4n, 5n, and 6n rules : [англ.]. — Urbana-Champaign : University of Illinois, 2008.
↑ Gillespie, R. J. Nyholm Memorial Lectures : [англ.] // Chemical Society Reviews. — 1979. — Vol. 8, no. 3. — P. 315–352. — doi:10.1039/CS9790800315.
↑ Mingos, D. Michael P. Polyhedral Skeletal Electron Pair Approach : [англ.] // Accounts of Chemical Research. — 1984. — Vol. 17, no. 9. — P. 311–319. — doi:10.1021/ar00105a003.
↑ Cotton et al., 1999.
↑ Cotton, 1990, p. 205–251.

Литература

Greenwood, Norman N. Chemistry of the Elements : [англ.] / Norman N. Greenwood, Alan Earnshaw. — 2nd ed. — Butterworth-Heinemann, 1997. — ISBN 978-0-08-037941-8.
Cotton, F. Albert. Advanced Inorganic Chemistry : [англ.] / F. Albert Cotton, Geoffrey Wilkinson, Carlos A. Murillo … [et al.]. — 6th ed. — New York : Wiley-Interscience, 1999. — ISBN 0-471-19957-5.
Cotton, Albert. Chemical Applications of Group Theory : [англ.]. — John Wiley & Sons, 1990. — ISBN 0-471-51094-7.