Джон Форбс Нэш-младший — американский математик, работавший в области теории игр, дифференциальной геометрии и изучения уравнений в частных производных. Его теории широко используются в экономике.
Тео́рия игр — математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более стороны, ведущие борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их ресурсах и их возможных поступках.
Равнове́сие Нэ́ша — концепция решения, одно из ключевых понятий теории игр. Так называется набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники своих стратегий не меняют. Джон Нэш доказал существование такого равновесия в смешанных стратегиях в любой конечной игре.
Игра с полной информацией — теоретико-игровой термин, обозначающий игру, в которой игрокам известны функция полезности, правила игры, а также ходы других игроков. Примеры игр c полной информацией — шахматы и нарды; с неполной информацией — аукцион и покер.
Кооперативная теория игр занимается изучением игр, в которых группы игроков — коалиции — могут объединять свои усилия. Этим она отличается от некооперативных игр, в которых коалиции неприемлемы и каждый обязан играть за себя.
В теории игр страте́гия игрока в игре или деловой ситуации — это полный план действий при всевозможных ситуациях, способных возникнуть. Стратегия определяет действие игрока в любой момент игры и для каждого возможного течения игры, способного привести к каждой ситуации.
Дифференциальные игры — раздел математической теории управления, в котором изучается управление объектом в конфликтных ситуациях. В дифференциальных играх возможности игроков описываются дифференциальными уравнениями или дифференциальными включениями, содержащими управляющие векторы, которыми распоряжаются игроки. Для выбора своего управления каждый игрок может использовать лишь текущую информацию о поведении игроков. Различают дифференциальные игры двух игроков и многих игроков.
Математические методы в экономике — научное направление в экономике, посвящённое исследованию экономических систем и процессов с помощью математических моделей.
Антагонисти́ческая игра́ или игра́ с нулево́й су́ммой — термин теории игр. Антагонистической игрой называется некооперативная игра, в которой сумма выигрышей и проигрышей всех игроков равна 0. Следовательно, это означает, что выигрыш одного обязательно представляет собой проигрыш для другого.
Игрок в теории игр — рациональный индивид, имеющий заинтересованность в исходе игры и возможности воздействовать на него.
Некооперативная игра — термин теории игр. Некооперативной игрой называется математическая модель взаимодействия нескольких сторон (игроков), в процессе которого они не могут формировать коалиции и координировать свои действия.
Равновесие дрожащей руки — принцип оптимальности в некооперативных играх, представляющий собой равновесие Нэша, обладающее дополнительным свойством устойчивости к достаточно малым отклонениям игроков от равновесных стратегий. Сформулировано Р. Зельтеном в работе 1975 года.
Подыгра в теории игр — любая часть игры в развернутой форме, удовлетворяющая следующим условиям:
- имеет одну начальную позицию, находящуюся в одноточечном информационном множестве;
- содержит все позиции исходной игры, следующие за любой содержащейся в ней позицией;
- содержит все элементы информационных множеств, если в неё входит хотя бы один их элемент.
ε-равновесие в теории игр — профиль стратегий игроков некооперативной игры, приблизительно удовлетворяющий условиям равновесия Нэша.
Домини́рование в теории игр — ситуация, при которой одна из стратегий некоторого игрока дает больший выигрыш, нежели другая, при любых действиях его оппонентов. Обратное понятие, нетранзитивность, возникает, если некоторая стратегия может давать меньшие выигрыши, чем другая, в зависимости от поведения остальных участников.
Сильное равновесие — принцип оптимальности в теории игр, очищение равновесия Нэша. Кроме устойчивости ситуации в игре к индивидуальным отклонениям участников, требует также устойчивости к групповым отклонениям.
В теории игр, игра в нормальной или стратегической форме состоит из трех элементов: множества игроков, множества чистых стратегий каждого игрока, множества платежных функций каждого игрока. Таким образом, игру в нормальной форме можно представить в виде n-мерной матрицы (таблицы), элементы которой это n-мерные платежные вектора. Эта таблица называется платёжной матрицей.
Доминирование по риску и доминирование по выигрышу — две взаимосвязанных концепции решения в теории некооперативных игр, являющихся рафинирование равновесия Нэша. Введены Дж. Харшаньи и Р. Зелтеном.
Александр Алексеевич Васин — математик, доктор физико-математических наук, профессор факультета ВМК МГУ. Ведущий российский специалист в области теории некооперативных игр и её применений к экономике и биологии.
Игра с совершенной информацией — игра, в которой игроки в ходе игры не сталкиваются ни со стратегической неопределённостью, ни с внешней неопределённостью. Таким образом, в игре с совершенной информацией каждый игрок в каждой точке, в которой наступает его очередь ходить, знает всю историю игры вплоть до этой точки, в том числе результаты любых действий, предпринятых «природой», или предыдущие действия других игроков, включая чистые стратегии и фактические результаты любых смешанных стратегий, которые они могут использовать в игре.
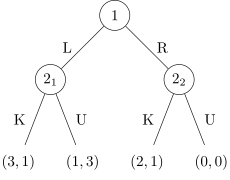Игра в развёрнутой форме
Равновесие Нэша, несовершенное по подыграм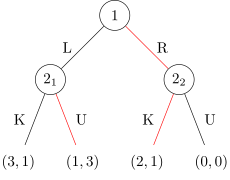
Равновесие, совершенное по подыграм
