
Го́тфрид Ви́льгельм Ле́йбниц — немецкий философ, логик, математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук, член Лондонского королевского общества (1673), иностранный член Французской Академии наук.

Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством разнообразных вычислений. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач. Современная вычислительная математика включает в круг своих проблем изучение особенностей вычисления с применением компьютеров.
Математи́ческий ана́лиз — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное и интегральное исчисления.

Барон Огюсте́н Луи́ Коши́ — французский математик и механик, член Парижской академии наук, Лондонского королевского общества, Петербургской академии наук и других академий.

Жан Леро́н Д’Аламбе́р — французский учёный-энциклопедист. Широко известен как философ, математик и механик.
А́лгебра Ли — объект общей алгебры, являющийся векторным пространством с определенной на ней антикоммутативной билинейной операцией, удовлетворяющей тождеству Якоби. В общем случае алгебра Ли является неассоциативной алгеброй. Названа по имени норвежского математика Софуса Ли (1842—1899).

Фердина́нд Гео́рг Фробе́ниус — немецкий математик, известный своим вкладом в теорию эллиптических функций, дифференциальных уравнений и теории групп. Он также был первым, кто ввёл понятие рациональной аппроксимации функций, и дал первое полное доказательство теоремы Гамильтона — Кэли. Также он внёс свой вклад в определение дифференциально-геометрических объектов в современной математической физике, известных ныне как многообразия Фробениуса.
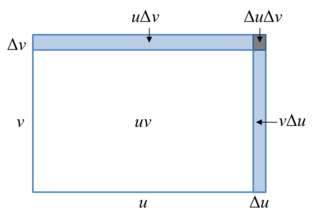
Правило произведения, или тождество Лейбница, — характерное свойство дифференциальных операторов.


Абраха́м де Муа́вр — английский математик французского происхождения.

Влади́мир Алекса́ндрович Ильи́н — советский и российский математик, профессор МГУ, академик АН СССР (1990) и РАН. Внёс заметный вклад в теорию дифференциальных уравнений, спектральную теорию дифференциальных операторов и математическое моделирование.
Существует несколько математических и физических объектов, названных в честь Исаака Ньютона:
Ряд Лейбница — знакочередующийся ряд, названный именем исследовавшего его немецкого математика Лейбница :

Численные (вычислительные) методы — методы решения математических задач в численном виде.

Ве́кторное исчисле́ние — раздел математики, в котором изучаются свойства операций над векторами.
Анализ бесконечно малых — историческое название математического анализа, раздела высшей математики, изучающего пределы, производные, интегралы и бесконечные ряды, и составляющего важную часть современного математического образования. Состоит из двух основных частей: дифференциального исчисления и интегрального исчисления, которые связаны между собой формулой Ньютона — Лейбница.
Анализ — объединение нескольких разделов математики, исторически выросшее из классического математического анализа и охватывающее, кроме дифференциального и интегрального исчислений, входящих в классическую часть, такие разделы, как теории функций вещественной и комплексной переменной, теории дифференциальных и интегральных уравнений, вариационное исчисление, гармонический анализ, функциональный анализ, теорию динамических систем и эргодическую теорию, глобальный анализ. Нестандартный анализ находится на стыке математической логики и анализа, применяет методы теории моделей для альтернативной формализации, прежде всего, классических разделов.

Спор Ньютона и Лейбница о приоритете — спор о приоритете открытия дифференциального и интегрального исчисления между Исааком Ньютоном (1642—1727) и Готфридом Вильгельмом Лейбницем (1646—1716). Свою версию теории Ньютон создал ещё в 1665—1666 годах, однако не публиковал её до 1704 года. Независимо от него Лейбниц разработал свой вариант дифференциального исчисления, хотя первоначальный толчок, вероятно, его мысль получила из слухов о том, что такое исчисление у Ньютона уже имеется, а также благодаря научным беседам в Англии и переписке с Ньютоном. В отличие от Ньютона, Лейбниц сразу опубликовал свою версию и в дальнейшем, вместе с Якобом и Иоганном Бернулли, широко пропагандировал это открытие по всей Европе. Большинство учёных на континенте не сомневались, что анализ открыл Лейбниц. Когда Ньютон решил опубликовать свои труды на эту тему, возник вопрос о приоритете совершённого открытия. Ожесточённый спор не завершился со смертью Лейбница и продолжался усилиями сторонников основных участников, прекратившись только со смертью Ньютона.
Список объектов, названных в честь французского математика XIX века Огюстена Луи Коши.
- Горизонт Коши
- Задача Коши — задача нахождения решения дифференциального уравнения, удовлетворяющего начальным условиям.
- Интеграл Коши — Лагранжа — интеграл уравнений движения идеальной жидкости в случае потенциальных течений.
- Интегральная теорема Коши — интеграл от аналитической функции по замкнутой кривой в односвязной области равен нулю.
- Интегральная формула Коши — соотношение для голоморфных функций комплексного переменного, связывающее значение функции в точке с её значениями на контуре, окружающем точку.
- Интегральный признак Коши — Маклорена — признак сходимости убывающего положительного числового ряда.
- Коши — небольшой ударный кратер на видимой стороне Луны.
- Критерий Коши равномерной сходимости несобственных интегралов.
- Критерий сходимости Коши — критерий сходимости числовых рядов.
- Лемма Коши — Фробениуса — классический результат комбинаторной теории групп, даёт выражение на число орбит в действии группы.
- Матрица Коши
- Матрица Коши — матрица, с помощью которых выражаются решения систем неоднородных дифференциальных уравнений.
- Неравенство Коши — Буняковского — обобщение неравенства треугольника, связывает норму и скалярное произведение векторов в евклидовом или гильбертовом пространстве.
- Неравенство Коши — соотношение среднего арифметического, среднего геометрического, среднего гармонического и среднего квадратического.
- Принцип Коши — Кантора — лемма о вложенных отрезках, доказывающая полноту множества вещественных чисел.
- Радикальный признак Коши — признак сходимости числового ряда.
- Распределение Коши — класс вероятностных распределений.
- Телескопический признак Коши — признак сходимости положительных числовых рядов.
- Тензор деформации Коши-Грина — тензор, который характеризует сжатие (растяжение) и изменение формы в каждой точке тела при деформации.
- Тензор напряжений Коши — тензор, описывающий механические напряжения в произвольной точке нагруженного тела при малых деформациях.
- Теоре́ма Больцано — Коши — если непрерывная функция, определённая на вещественном промежутке, принимает два значения, то она принимает и любое значение между ними.
- Теорема Коши о вычетах — даёт способ вычисления интеграла мероморфной функции по замкнутому контуру.
- Теорема Коши — Адамара о степенном ряде — оценка радиуса сходимости некоторых степенных рядов.
- Теорема Коши — Дэвенпорта в аддитивной комбинаторике: размер множества сумм двух множеств в группе вычетов
 никогда не оказывается существенно меньше, чем сумма их размеров.
никогда не оказывается существенно меньше, чем сумма их размеров. - Теорема Коши — Ковалевской — теорема о существовании и единственности локального решения задачи Коши для дифференциального уравнения в частных производных.
- Теорема Коши о многогранниках — грани многогранника вместе с правилом склейки полностью определяют выпуклый многогранник.
- Теорема Коши о среднем значении — обобщение формулы конечных приращений.
- Теорема Коши — Пеано — теорема о существовании решения обыкновенного дифференциальное уравнения.
- Теорема Коши — Пуанкаре — обобщение на случай многомерного комплексного пространства интегральной теоремы Коши.
- Теорема Коши — если порядок конечной группы
 делится на простое число
делится на простое число  , то
, то  содержит элементы порядка
содержит элементы порядка  .
. - Уравнение Коши - Эйлера — вид линейного дифференциального уравнения, допускающего простой алгоритм решения.
- Условия Коши — Римана — соотношения, связывающие вещественную и мнимую части всякой дифференцируемой функции комплексного переменного.
- Формула Бине — Коши — теорема об определителе произведения двух матриц, которое является квадратной матрицей
- Фундаментальная последовательность Коши — последовательность точек метрического пространства такая, что для любого ненулевого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии менее, чем заданное.
- Условие Коши — критерий сходимости фундаментальной последовательности Коши.
- Функциональное уравнение Коши
- Число Коши — критерий подобия в механике сплошных сред.




















