
Гомеоморфи́зм — непрерывная биекция с непрерывной обратной. Является центральным понятием топологии.
Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

Лине́йно свя́зное простра́нство — топологическое пространство, в котором любые две точки можно соединить непрерывной кривой.
Теорема Больцано — Вейерштрасса, или лемма Больцано — Вейерштрасса о предельной точке, — предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства  можно выделить сходящуюся подпоследовательность. Теорема Больцано — Вейерштрасса, в особенности случай числовой последовательности, входит в каждый курс анализа. Она используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема носит имена чешского математика Больцано и немецкого математика Вейерштрасса, которые независимо друг от друга её сформулировали и доказали.
можно выделить сходящуюся подпоследовательность. Теорема Больцано — Вейерштрасса, в особенности случай числовой последовательности, входит в каждый курс анализа. Она используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема носит имена чешского математика Больцано и немецкого математика Вейерштрасса, которые независимо друг от друга её сформулировали и доказали.
Равноме́рная непреры́вность — это свойство функции быть одинаково непрерывной во всех точках области определения. В математическом анализе это понятие вводится для числовых функций, в функциональном анализе оно обобщается на произвольные метрические пространства.
Непрерывная функция — функция, которая меняется без мгновенных «скачков», то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.
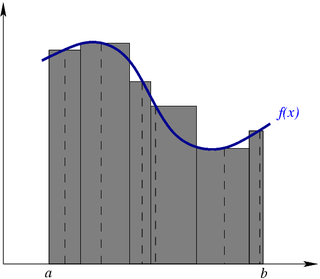
Интегра́л Ри́мана — наиболее широко используемый вид определённого интеграла. Очень часто под термином «определённый интеграл» понимается именно интеграл Римана, и он изучается самым первым из всех определённых интегралов во всех курсах математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.
Норма — функционал, заданный на векторном пространстве и обобщающий понятие длины вектора или абсолютного значения числа.

Голоморфная функция, иногда называемая регулярной функцией — функция комплексного переменного, определённая на открытом подмножестве комплексной плоскости  и комплексно дифференцируемая в каждой точке.
и комплексно дифференцируемая в каждой точке.

Теорема о промежуточном значении утверждает, что если непрерывная функция, определённая на вещественном промежутке, принимает два значения, то она принимает и любое значение между ними.
Теоре́ма Вейерштра́сса — теорема математического анализа и общей топологии, которая гласит, что функция, непрерывная на компакте, ограничена на нём и достигает своих точных верхней и нижней граней.
Ле́мма Фату́ — техническое утверждение, используемое при доказательстве различных теорем в функциональном анализе и теории вероятностей. Оно даёт одно из условий, при которых предел почти всюду сходящейся функциональной последовательности будет суммируемым.
Критической точкой дифференцируемой функции  называется точка, в которой её дифференциал обращается в нуль. Это условие эквивалентно тому, что в данной точке все частные производные первого порядка обращаются в нуль, геометрически оно означает, что касательная гиперплоскость к графику функции горизонтальна. В простейшем случае n=1 это значит, что производная
называется точка, в которой её дифференциал обращается в нуль. Это условие эквивалентно тому, что в данной точке все частные производные первого порядка обращаются в нуль, геометрически оно означает, что касательная гиперплоскость к графику функции горизонтальна. В простейшем случае n=1 это значит, что производная  в данной точке равна нулю. Это условие является необходимым для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума дифференцируемой функции.
в данной точке равна нулю. Это условие является необходимым для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума дифференцируемой функции.
Абсолютная непрерывность — свойство функций и мер, состоящее, неформально говоря, в выполнении теоремы Ньютона — Лейбница о связи между интегрированием и дифференцированием. Обычно эта теорема формулируется в терминах интеграла Римана и включает в свои условия интегрируемость производной по Риману. При переходе к более общему интегралу Лебега естественное требование существования измеримой производной почти всюду становится слишком слабым, и для выполнения соотношения, аналогичного теореме Ньютона — Лейбница, необходимо более тонкое условие, которое и называется абсолютной непрерывностью. Это понятие переносится на меры с помощью производной Радона — Никодима.

Формула Ньютона — Лейбница, или основная формула анализа, или формула Барроу даёт соотношение между двумя операциями: взятием интеграла Римана и вычислением первообразной.
Правило дифференцирования сложной функции позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных.

Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция  .
.
Теорема об обратной функции даёт достаточные условия для существования обратной функции в окрестности точки через производные от самой функции.
![{\displaystyle f:[a,b]\subset \mathbb {R} \to \mathbb {R} ,\;f\in C^{0}{\bigl (}[a,b]{\bigr )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea7db075924b0ead08afd1b8301ac2d02bb3b309)

![{\displaystyle f{\bigl (}[a,b]{\bigr )}=[c,d].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44edcd5a84d62f06673de042540c2a9044d97695)


![{\displaystyle f:[0,1]\to \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bafb1e62d4de21640d672bb803a68771832b379)
![{\displaystyle f(x)=\left\{{\begin{matrix}\sin \left({\frac {\pi }{2x}}\right),&x\in (0,1]\\0,&x=0\end{matrix}}\right..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f00e028dffc37ef67209fb4c8c9730fd4e9c2400)

![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
![{\displaystyle F:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cacd74b0bb95ed9ddf45676b1ad0f3d618c4cdc)






![{\displaystyle f{\bigl (}[a,b]{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98bb8617481c8a74b87b45e322eae869304858bc)




















