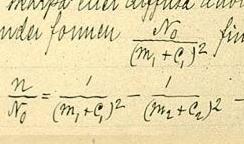Тормозное излучение

Тормозно́е излуче́ние — электромагнитное излучение, испускаемое заряженной частицей при её рассеянии (торможении) в электрическом поле. Иногда в понятие «тормозное излучение» включают также излучение релятивистских заряженных частиц, движущихся в макроскопических магнитных полях (в ускорителях, в космическом пространстве), и называют его магнитотормозным; однако более употребительным в этом случае является термин «синхротронное излучение». Интересно, что немецкое слово Bremsstrahlung прочно закрепилось в английском языке.
Согласно классической электродинамике, которая достаточно хорошо описывает основные закономерности тормозного излучения, его интенсивность пропорциональна квадрату ускорения заряженной частицы. Так как ускорение обратно пропорционально массе m частицы, то в одном и том же поле тормозное излучение легчайшей заряженной частицы — электрона будет, например, в миллионы раз мощнее излучения протона (). Поэтому чаще всего наблюдается и практически используется тормозное излучение, возникающее при рассеянии электронов в электростатическом поле атомных ядер и электронов, такова, в частности, природа рентгеновских лучей в рентгеновских трубках и гамма-излучения, испускаемого быстрыми электронами при прохождении через вещество.
Причиной значительного тормозного излучения может быть тепловое движение в горячей разреженной плазме[1]. Элементарные акты тормозного излучения, называются в этом случае тепловым, обусловлены столкновениями заряженных частиц, из которых состоит плазма. Мощность тормозного излучения полностью ионизированной плазмы есть[2]:
- где — удельная мощность, эрг/сек/см3;
- — порядковый номер элемента;
- — концентрации электронов и ионов, см−3;
- — температура электронной плазмы, К.
Например, один литр водородной плазмы с электронной температурой 1⋅108 К и концентрацией электронов 1⋅1016 см-3 будет излучать рентгеновское излучение мощностью около 150 кВт[2]. Космическое рентгеновское излучение, наблюдение которого стало возможным с появлением искусственных спутников Земли, частично является, по-видимому, тепловым тормозным излучением.
Тормозное рентгеновское и гамма-излучение широко применяются в технике, медицине, в исследованиях по биологии, химии и физике.
История
Вероятно, впервые тормозное излучение наблюдал Никола Тесла в конце 19-го века, однако его результаты не получили широкой огласки[3]. В 1895 году, Вильгельм Рентген показал, что пучок электронов в вакуумной лампе порождает излучения (гамма-лучи) при столкновении с веществом (например, веществом самой лампы)[4]. В 1915 году Уильямом Дуэйном и Франклином Хантом была установлена эмпирическая зависимость максимальной энергии фотонов в зависимости от энергии падающих электронов[5]. В 1922 году Хельмут Куленкампф открыл, что спектр тормозного излучения является сплошным, а также описал его форму[6]. Первая (классическая) теория тормозного излучения была разработана Хендриком Крамерсом вскоре после этого.
Теория тормозного излучения, учитывающая квантовомеханические эффекты, была разработана Зоммерфельдом в 1929 году[6].
Теории тормозного излучения
Классическая теория
В классической электродинамике любой ускоренно движущийся заряд, будет создавать электромагнитные волны. Ускорение, которое ядро с зарядом придает частице с зарядом и массой пропорционально Тогда интенсивность излучения будет пропорциональной [5]. Таким образом, с одной стороны, интенсивность излучения пропорциональна квадрату атомного номера элемента, на котором тормозятся частицы. С другой стороны, интенсивность излучения сильно зависит от массы рассеиваемой частицы. Из-за этого, излучение, создаваемое протонами или альфа-частицами имеет интенсивность в миллионы раз меньше, чем для электронов, при рассеянии на том же веществе. Даже самая лёгкая частица, тяжелее электрона, мюон — в 212 раз тяжелее его, и следовательно, порождает в 40 000 раз менее интенсивное излучение. Поэтому, на практике, рассматривается только тормозное излучение, создаваемое электронами или позитронами.
Квантовая электродинамика
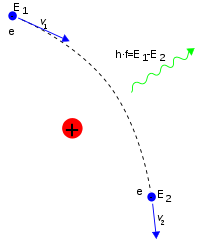
В квантовой теории электрон в кулоновском поле имеет некоторую вероятность перейти в состояние с более низкой энергией, испуская при этом фотон (существует вероятность образования нескольких фотонов в этом процессе, однако она крайне мала[7]). Этот процесс, по сути, является неупругим рассеянием электрона на ядре. Возможно и упругое рассеяние, при котором энергия электрона не меняется, и фотон не излучается, причём большинство актов рассеяния являются именно такими (для электронов с малой энергией и лёгких ядер, только 1/137 (постоянная тонкой структуры) от всех актов рассеивания является неупругими[5]).
Эта вероятность, в общем случае, зависит от энергии самого электрона. В нерелятивистском приближении, сечение излучения фотона с энергией для электрона, пролетающего на расстоянии от ядра равна[8]:
- где — заряд ядра,
- — энергия покоя электрона,
- — кинетическая энергия электрона,
- и — импульс электрона до и после столкновения.
Таким образом, в первом приближении можно сказать, что вероятность образования фотона обратно пропорциональна его энергии. С другой стороны, в крайнем случае сверхвысоких энергий, распределение задаётся следующим образом[9]:
Как можно видеть, в обоих случаях существует зависимость вероятности излучения от
Также, на вид формул, описывающих тормозное излучение влияет искажения кулоновского поля электронными оболочками атома[9].
Во время рассеяния электрон может испустить любое количество энергии, вплоть до его полной кинетической энергии в зависимости от того, насколько близко от ядра он прошёл, и насколько сильно изменилась его траектория. Таким образом, максимальная частота тормозного излучения определяется уравнением [5], из которого следует: , где V — напряжение, ускоряющее электрон. Это уравнение называется пределом Дуэйна — Ганта[англ.]. Это является одним из важных отличий распределения энергий, предполагаемым в классической теории, от того, что предусматривает квантово-механическая теория — в классической теории тормозное излучение охватывает весь спектр[10].
Угловое распределение излучения
Угловое распределение тормозного излучения зависит от кинетической энергии падающих электронов. В случае релятивистских электронов, направления вылета фотонов преимущественно находятся в конусе с углом при вершине (это значение является средним углом вылета фотонов). Угловое распределение в таком случае принимает вид[11]:
Для нерелятивистских электронов, фотоны могут испускаться как вперед, так и назад, их угловое распределение пропорционально где — угол между направлением вылета фотона и траекторией тормозящегося электрона.
Поляризация
Если электрон тормозится по линейному закону, то его излучение будет полностью поляризовано. Однако, тормозное излучение в веществе создаётся электронами, движущимися по гиперболическим траекториям, поэтому поляризация происходит лишь частично. Чем ближе к ядру пролетает электрон, тем сильнее меняется его траектория, а значит, тем больше компонента ускорения, направленная в противоположную от движения сторону. Таким образом, есть два случая почти полной поляризации тормозного излучения: когда электрон проходит очень близко от ядра, и практически останавливается (в этом случае векторы скорости и тормозящего поля практически параллельны), что соответствует зоне, близкой к коротковолнового лимита фотонов, или когда он проходит относительно далеко от ядра (тогда векторы скорости и поля перпендикулярны, то есть поляризация является отрицательной), что соответствует наименее энергетическим фотонам[12]. В промежуточных случаях поляризация меньше.
Общая поляризация тормозного излучения составляет около 50 %.
Спектр тормозного излучения

Спектр тормозного излучения непрерывный, а его максимальная частота определяется энергией заряженной частицы. Если электрон ускорить в потенциале в десятки киловольт, то при торможении такого электрона возникнут электромагнитные волны в рентгеновском диапазоне.
Форма спектра является сложной, но общие принципы следующие: доля фотонов заданной частоты уменьшается с ростом частоты, и стремится к нулю при приближении к максимальному её значению. Для более высокоэнергетических электронов, количество фотонов, энергия которых близка к максимально возможной, растёт, что выражается всплеском на графике спектра при энергиях фотонов приближающихся к энергиям налетающих электронов[13].
Хорошим приближением спектра тормозного излучения является формула Крамерса[англ.] [14]:
- где — минимальная длина волны излучения,
- — некоторый коэффициент, зависящий от материала мишени.
Практически спектр фотонов подавляется в низкочастотной области, потому что поглощение низкоэнергетических фотонов в веществе значительно сильнее, чем высокоэнергетических[15].
Интенсивность
При пролёте через слой вещества толщиной dx, состоящий из атомов с зарядом и массовым числом электрон излучает некоторую долю своей энергии что выражается следующей эмпирической формулой[16]:
- где имеет размерность г/см2.
Из формулы видно, что энергия электронов и интенсивность тормозного излучения спадают экспоненциально при углублении в мишень. Толщина слоя вещества, при пролёте через которую энергия электрона уменьшается в e раз называется радиационной длиной. Эта величина часто используется для измерения толщины мишеней.
Поскольку гамма-излучения также поглощается в веществе, для максимизации интенсивности излучения, толщина мишени должна быть не очень большой. Обычно, излучение достигает максимума при толщине слоя вещества в 1/3—1/4 от максимального пробега.
Источники
Рентгеновские трубки
В рентгеновских трубках электроны разгоняются электрическим полем, после чего ударяются в специальную металлическую мишень. Во время столкновений с атомами мишени, электроны тормозятся, и излучают фотоны, в том числе и в рентгеновском диапазоне. Не всё излучения рентгеновских трубок является тормозным — большая его часть приходится на характеристическое рентгеновское излучение — передачи энергии электрона, что переводит его на более высокую орбиталь, и дальнейшее его возвращения на нижней энергетический уровень с излучением полученной энергии.
Благодаря своей простоте и доступности, эта схема очень часто применяется для искусственного получения рентгеновских лучей, и используется в медицине и технике, несмотря на то, что её КПД достаточно низкий — всего 3-8 % энергии превращается в рентгеновское излучение[17].
Бета-распад
Одним из продуктов бета-распада является бета-частица — высокоэнергетический электрон. При прохождении бета-частиц через вещество они теряют энергию через тормозное излучение, и этот канал является тем больше, чем больше энергия частицы. Кроме обычного тормозного излучения, образующегося при движении электрона в веществе (внешнее тормозное излучение), существует другой подвид излучения, характерное для бета-распада — внутреннее тормозное излучение, состоящее из гамма-квантов, которые образуются непосредственно при бета-распаде[18]. Поскольку энергия бета-частиц ограничена, заметным тормозное излучение становится лишь для очень интенсивных источников бета-излучения.
Тормозное излучение следует учитывать при разработке защиты от бета-радиации, ведь гамма-лучи имеют значительно большую проникающую способность чем бета-частицы, для защиты от которых достаточно металлического экрана толщиной в несколько миллиметров. Для защиты от высокоэнергетических бета-частиц следует использовать экраны из пластика или других материалов, состоящих из элементов с низким атомным номером, для уменьшения вероятности излучения высокоэнергетических фотонов[19].
Тепловое движение
В плазме атомы являются ионизированными, а следовательно присутствует большое количество свободных носителей заряда. Тормозное излучение в таком случае возникает при столкновении электронов и ионов. С увеличением температуры, скорости электронов и, соответственно, энергии фотонов растут.
Если плазма является прозрачной для излучения, то тормозное излучение является эффективным способом её охлаждения. Такой канал является основным для температур, превышающих 10 000 000 кельвинов[20].
Именно такое излучение является основной причиной радиоизлучения солнечной короны, планетарных туманностей и межзвездного газа[21].
Электрон-электронное рассеяние
Электрон может рассеиваться и на электронных оболочках атомов. Это излучение значительно меньше того, что генерируется при рассеянии на ядрах, поскольку заряд электрона составляет лишь 1e, тогда как энергия тормозного излучения пропорциональна квадрату заряда частицы-мишени. При энергиях падающих электронов меньших 300 кэВ этим каналом можно пренебречь[22]. Однако с ростом скорости электронов, а также для легких элементов (заряд ядра которых не такой большой по сравнению с зарядом электрона), например, при прохождении через воздух, его значимость возрастает. Электрон-электронное тормозное излучение является значительным в некоторых астрофизических процессах, в облаках плазмы с температурой большей 109 К[21].
Нуклонное тормозное излучение
Как было сказано выше, интенсивность тормозного излучения, создаваемого протонами в кулоновском поле, в несколько миллионов раз меньше излучения, создаваемого электронами, потому что оно обратно пропорционально квадрату массы. Однако, нуклон-нуклонные силы значительно больше электромагнитных, а потому тормозное излучение нуклонами было зафиксировано в ядерных реакциях, таких как:
- p + n → 2 H + γ,
или:
- p + 2 H → 3 He + γ.
Фотоны, излучаемые в таких реакциях, имеют энергию в несколько МэВ[23].
Примечания
- ↑ Элементарная физика плазмы, 1969, с. 84.
- ↑ 1 2 Элементарная физика плазмы, 1969, с. 85.
- ↑ Nikola Tesla: Lecture Before The New York Academy of Sciences — April 6, 1897 Архивная копия от 16 февраля 2017 на Wayback Machine (англ.)
- ↑ Bremsstrahlung & X-Rays Архивная копия от 25 ноября 2013 на Wayback Machine (англ.)
- ↑ 1 2 3 4 THE ATOMIC NUCLEUS Архивная копия от 29 мая 2015 на Wayback Machine (англ.)
- ↑ 1 2 Scintillation Spectrometry of Low-Energy Bremsstrahlung Архивная копия от 16 января 2017 на Wayback Machine (англ.)
- ↑ тормозное излучение Архивная копия от 7 января 2017 на Wayback Machine (рус.)
- ↑ Квантовая теория излучения, 1956, p. 280.
- ↑ 1 2 Квантовая теория излучения, 1956, p. 281.
- ↑ Тормозное рентгеновское излучение Архивная копия от 18 января 2017 на Wayback Machine (рус.)
- ↑ Электромагнитные взаимодействия заряженных частиц Архивная копия от 28 ноября 2016 на Wayback Machine (рус.)
- ↑ Основы физики рентгеновского излучения, 2007, p. 54.
- ↑ 1 2 Активационный анализ, 1974, p. 111.
- ↑ Основы физики рентгеновского излучения, 2007, p. 65.
- ↑ Получение и применение радиоактивных изотопов, 1962, p. 65.
- ↑ Тормозное излучение Архивная копия от 18 января 2017 на Wayback Machine (рус.)
- ↑ EFFECTIVE X-RAY BREMSSTRAHLUNG SOURCE Архивная копия от 25 мая 2017 на Wayback Machine (англ.)
- ↑ Краткая химическая энциклопедия, 1962, p. 91.
- ↑ Shielding Beta radiation to reduce Bremsstrahlung Архивная копия от 18 января 2017 на Wayback Machine (англ.)
- ↑ Солнечно-земная физика, 2009, p. 110.
- ↑ 1 2 Тормозное излучение Архивная копия от 21 января 2017 на Wayback Machine (рус.)
- ↑ ELECTRON-ELECTRON BREMSSTRAHLUNG EMISSION AND THE INFERENCE OF ELECTRON FLUX SPECTRA IN SOLAR FLARES Архивная копия от 25 июля 2018 на Wayback Machine (англ.)
- ↑ Radioactivity: Introduction and History, From the Quantum to Quarks, 2016, p. 282.
Литература
- Гайтлер В. Радиационные процессы в первом приближении // Квантовая теория излучения. — 3. — М.: "Издательство иностранной литературы", 1956. — С. 280. — 498 с. — ISBN 5-4584-2739-4.
- Кузнецов Р. А. Нормированные спектры тормозного излучения для разных энергий электронов // Активационный анализ. — 2. — М.: АТОМИЗДАТ, 1974. — С. 111. — 344 с.
- Гелий Павлинский. Тормозное рентгеновское излучение // Основы физики рентгеновского излучения. — М.: Физматлит, 2007. — С. 47. — 239 с. — ISBN 5-4579-6651-8.
- Бочкарёв В. В. Применение радиоактивных изотопов // Получение и применение радиоактивных изотопов. — М.: Госатомиздат, 1962. — 288 с.
- Кнунянц И. Л. Защита от излучений радиоактивных веществ // Краткая химическая энциклопедия. — М.: "Советская энциклопедия", 1962. — Т. 2. — С. 91. — 1082 с. — ISBN 5-4582-6128-3.
- Исследование активных процессов в солнечной короне // Солнечно-земная физика. — М.: Физматлит, 2009. — 488 с. — ISBN 978-5-9221-1175-1.
- Michael F. L'Annunziata. Bremsstrahlung // Radioactivity: Introduction and History, From the Quantum to Quarks. — 2. — ELSEVIER, 2016. — 903 с. — ISBN 978-0-4446-3496-2.
- Арцимович Л. А. Элементарная физика плазмы. — 3-е изд. — М.: Атомиздат, 1969. — 189 с.
- Котельников И. А. Лекции по физике плазмы. Том 1: Основы физики плазмы. — 3-е изд. — СПб.: Лань, 2021. — 400 с. — ISBN 978-5-8114-6958-1.


















![{\displaystyle \phi _{k}d\left({\frac {k}{E_{0}}}\right)=2{\frac {Z^{2}r_{0}^{2}}{137}}{\frac {dk}{k}}{\frac {E}{E_{0}}}\left[{\frac {E_{0}^{2}+E^{2}}{E_{0}E}}-{\frac {2}{3}}\right]\left[2{\text{ln}}{\frac {2E_{0}E}{\mu k}}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7d6ea71371c79329781de25cd8bb5eda3f64175)