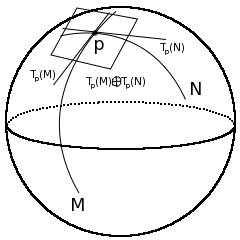
Риманово многообразие, или риманово пространство (M, g), — это (вещественное) гладкое многообразие M, в котором каждое касательное пространство снабжено скалярным произведением g — метрическим тензором, меняющимся от точки к точке гладким образом. Другими словами, риманово многообразие — это дифференцируемое многообразие, в котором касательное пространство в каждой точке является конечномерным евклидовым пространством.
Коэффициент зацепления — целочисленная характеристика пары пространственных замкнутых кривых без пересечений и самопересечений, описывающая суммарное количество раз, которое одна кривая в определённом смысле зацепляется за другую.
Производная — фундаментальное математическое понятие, используемое в различных вариациях (обобщениях) во многих разделах математики. Это базовая конструкция дифференциального исчисления, допускающая много вариантов обобщений, применяемых в математическом анализе, дифференциальной топологии и геометрии, алгебре.
Метри́ческий те́нзор, или ме́трика, — симметричное тензорное поле ранга (0,2) на гладком многообразии, посредством которого задаётся скалярное произведение векторов в касательном пространстве. Иначе говоря, метрический тензор задаёт билинейную форму на касательном пространстве к этой точке, обладающую свойствами скалярного произведения и гладко зависящую от точки.
Касательный вектор — элемент касательного пространства, например элемент касательной прямой к кривой, касательной плоскости к поверхности так далее.
Многообра́зие — локально евклидово пространство.
Вторая квадратичная форма поверхности ― квадратичная форма на касательном расслоении поверхности, которая, в отличие от первой квадратичной формы, определяет внешнюю геометрию поверхности в окрестности данной точки.
Формула Гаусса — выражение для гауссовой кривизны поверхности в трёхмерном римановом пространстве через главные кривизны и секционную кривизну объемлющего пространства. В частности, если объемлющее пространство евклидово, то гауссова кривизна поверхности равна произведению главных кривизн в этой точке.
Геодезическая кривизна  кривой
кривой  в римановой геометрии измеряет, насколько далеко кривая отличается от геодезической. Например, для 1D кривой на 2D поверхности, вложенной в 3D пространство, это кривизна кривой, спроецированной на плоскость, касательную к поверхности. Более обще, в заданном многообразии
в римановой геометрии измеряет, насколько далеко кривая отличается от геодезической. Например, для 1D кривой на 2D поверхности, вложенной в 3D пространство, это кривизна кривой, спроецированной на плоскость, касательную к поверхности. Более обще, в заданном многообразии  геодезическая кривизна ― это обычная кривизна кривой
геодезическая кривизна ― это обычная кривизна кривой  . Однако если кривая
. Однако если кривая  лежит в подмногообразии
лежит в подмногообразии  многообразия
многообразия  , геодезическая кривизна относится к кривизне
, геодезическая кривизна относится к кривизне  в
в  , и она отличается в общем виде от кривизны
, и она отличается в общем виде от кривизны  в объемлющем многообразии
в объемлющем многообразии  . (Объемлющая) кривизна
. (Объемлющая) кривизна  кривой
кривой  зависит от двух факторов ― кривизны подмногообразия
зависит от двух факторов ― кривизны подмногообразия  в направлении
в направлении  , которая зависит только от направления кривой и кривизны
, которая зависит только от направления кривой и кривизны  в многообразии
в многообразии  , которая является величиной второго порядка. Связь между ними ―
, которая является величиной второго порядка. Связь между ними ―  . В частности, геодезические на
. В частности, геодезические на  имеют нулевую геодезическую кривизну («прямые»), так что
имеют нулевую геодезическую кривизну («прямые»), так что  .
.

О́бщее положе́ние — свойство, которое выполняется почти всюду, то есть почти для всех рассматриваемых объектов. Математический термин, используемый в основном в геометрии, значение которого зависит от контекста и который применяется обычно в следующих словосочетаниях: «объекты, находящиеся в общем положении, имеют свойство S», «S есть свойство общего положения», «приведение объектов в общее положение», другими словами, между объектами отсутствуют какие-либо «особые» отношения.

Алгебраическое многообразие — центральный объект изучения алгебраической геометрии. Классическое определение алгебраического многообразия — множество решений системы алгебраических уравнений над действительными или комплексными числами. Современные определения обобщают его различными способами, но стараются сохранить геометрическую интуицию, соответствующую этому определению.
Поверхность Веронезе — алгебраическая поверхность в пятимерном проективном пространстве, которая реализуется как образ вложения Веронезе. Существует также обобщение вложения Веронезе на произвольные размерности проективных пространств. Названа в честь итальянского математика Джузеппе Веронезе.
Квадратичным дифференциалом на многообразии называется сечение симметрического квадрата его кокасательного расслоения. Чаще всего это словосочетание используется в контексте комплексных многообразий, и молчаливо подразумевается, что это сечение является голоморфным. Чрезвычайную важность квадратичные дифференциалы имеют в теории комплексных кривых, или же римановых поверхностей.

Клод Лебрю́н — североамериканский геометр, специалист в комплексной и дифференциальной геометрии, в первую очередь четырёхмерных многообразий, а также теории относительности. Профессор Университета штата Нью-Йорк в Стони-Бруке.
Голоно́ми́я — один из инвариантов связности в расслоении над гладким многообразием, сочетающий свойства кривизны и монодромии, и имеющий важное значение как в геометрии, так и геометризированных областях естествознания, таких как теория относительности и теория струн. Обыкновенно речь идёт о голономии связностей в векторном расслоении, хотя в равной степени имеет смысл говорить о голономии связности в главном расслоении или даже голономии связности Эресманна в локально тривиальном топологическом расслоении.
В этом глоссарии приведены определения основных терминов, использующихся в теории узлов. Курсивом выделены ссылки внутри глоссария.