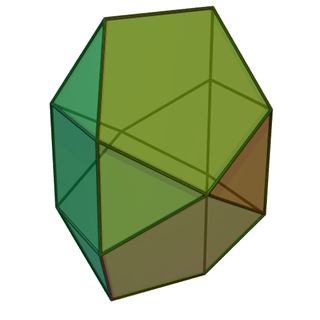
Трапецеромбический додекаэдр
| Трапецеромбический додекаэдр | |||
|---|---|---|---|
 | |||
| Свойства | выпуклый | ||
| Комбинаторика | |||
| Элементы |
| ||
| Грани | 6 ромбов 6 трапеций | ||
| Конфигурация вершины | 2(4.4.4) 6(4.4.4.4) 6(4.4.4) | ||
| Двойственный многогранник | трёхскатный прямой бикупол | ||
| Классификация | |||
| Группа симметрии | D3h | ||
Трапецеромби́ческий додека́эдр[1][2] — многогранник, двойственный трёхскатному прямому бикуполу.
Составлен из 12 граней: 6 равнобоких трапеций и 6 ромбов. Каждая грань окружена двумя трапециедальными и двумя ромбическими; у каждой грани два угла равны а два других
Имеет 14 вершин. В 2 вершинах сходятся своими тупыми углами три ромбических грани; в 6 вершинах (расположенных как вершины правильной треугольной призмы) сходятся острыми углами две трапециедальных и две ромбических грани; в остальных 6 (расположенных как вершины другой правильной треугольной призмы) сходятся тупыми углами две трапециедальных и одна ромбическая грани.
У трапецеромбического додекаэдра 24 ребра — 3 «длинных» (служащих большими основаниями трапеций), 18 «средних» (служащих боковыми сторонами трапеций и сторонами ромбов) и 3 «коротких» (служащих малыми основаниями трапеций). Двугранный угол при любом ребре одинаков и равен
Трапецеромбический додекаэдр можно получить из ромбододекаэдра, разрезав тот на две части любой плоскостью, пересекающей под прямыми углами шесть его рёбер, и повернув одну из частей на 60° вокруг её оси симметрии. Объём и площадь поверхности при этом не изменятся; вписанная и полувписанная сферы полученного многогранника также совпадают со вписанной и полувписанной сферами исходного ромбододекаэдра.
Метрические характеристики
Если «средние» рёбра трапецеромбического додекаэдра имеют длину , то его «длинные» рёбра имеют длину «короткие» — длину
Площадь поверхности и объём многогранника при этом выражаются как
Радиус вписанной сферы (касающейся всех граней многогранника в их инцентрах) при этом будет равен
радиус полувписанной сферы (касающейся всех рёбер) —
Описать около трапецеромбического додекаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.
Периметр любой грани будет равен
радиус окружности, вписанной в любую грань —
площадь любой грани —
Заполнение пространства
С помощью трапецеромбических додекаэдров можно замостить трёхмерное пространство без промежутков и наложений.
 Фрагмент заполнения
Фрагмент заполнения Рёберная модель
Рёберная модель
Данное заполнение является диаграммой Вороного для центров одинаковых сфер в шестиугольной плотной упаковке (ГП).
Примечания
- ↑ У. Болл, Г. Коксетер. Математические эссе и развлечения. — М.: Мир, 1986. — Стр. 164—165.
- ↑ М. Гарднер. Математические головоломки и развлечения. — М.: Мир, 1999. — Стр. 366—367.
Ссылки
- Weisstein, Eric W. Трапецеромбический додекаэдр (англ.) на сайте Wolfram MathWorld.