
Фигурные числа — числа, которые можно представить с помощью геометрических фигур. Это историческое понятие восходит к пифагорейцам, которые развивали алгебру на геометрической основе и представляли любое положительное целое число в виде набора точек на плоскости. Отголоском этого подхода остались выражения «возвести число в квадрат» или «в куб».

Шестиугольное число — фигурное число. n-ое шестиугольное число — число точек в состоящем из них правильном шестиугольнике со стороной в n точек.

Квадра́тное пирамида́льное число́ — пространственное фигурное число, представляющее пирамиду, с квадратным основанием. Квадратные пирамидальные числа также выражают количество квадратов со сторонами, параллельными осям координат, в решётке из N × N точек.

Пирамидальное число — пространственная разновидность фигурных чисел, представляющее пирамиду с многоугольным основанием и заданным числом треугольных боковых сторон. Уже античные математики исследовали тетраэдральные и квадратные пирамидальные числа, для которых в основании лежат правильный треугольник и квадрат соответственно. Несложно определить числа, связанные с пирамидами, в основании которых лежит любой другой многоугольник, например:

Центрированные шестиугольные числа – это центрированные фигурные числа, которые представляют шестиугольник с точкой в центре и все остальные окружающие точки находятся в шестиугольной решётке.
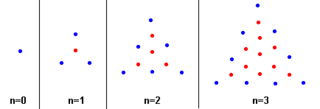
Центрированное треугольное число — это центрированное полигональное число, которое представляет треугольник с точкой в центре и все остальные окружающие точки находятся на треугольных слоях. Центрированное треугольное число для n задаётся формулой

Центрированное квадратное число — это центрированное полигональное число, которое представляет квадрат с точкой в центре и все остальные окружающие точки, находящиеся на квадратных слоях.

Центрированное пятиугольное число — это центрированное фигурное число, которое представляет пятиугольник, который содержит точку в центре и все точки, окружающие центр, лежат в пятиугольных слоях. Центрированное пятиугольное число для n задается формулой


Центрированное семиугольное число — это центрированное фигурное число, которое представляет семиугольник с точкой в середине и все окружающие точки лежат на семиугольных слоях. Центрированное семиугольное число для n задается формулой
 .
.

Центрированное десятиугольное число — центрированное фигурное число, которое представляет количество точек в десятиугольнике с точкой в середине и окружающими точками, лежащими на десятиугольных слоях. Центрированное десятиугольное число для n задаётся формулой

В теории чисел квадратным треугольным числом называется число, являющееся как треугольным, так и квадратным. Существует бесконечное число квадратных треугольных чисел.

Пятиугольные числа — один из классов классических многоугольных чисел. Последовательность пятиугольных чисел имеет вид :
- 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477…

Числа звёздчатого октаэдра — фигурные числа, подсчитывающие число шаров, которые можно расположить внутри звёздчатого октаэдра. Эти числа равны: 0, 1, 14, 51, 124, 245, 426, 679, 1016, 1449, 1990, … и в общем случае задаются уравнением  . Производящая функция чисел звёздчатого октаэдра:
. Производящая функция чисел звёздчатого октаэдра: 
Восьмиугольное число — разновидность многоугольных фигурных чисел, которая может быть представлена восьмиугольником. Общая формула n-го по порядку восьмиугольного числа: 3n2 — 2n, где  .
.

Семиугольные числа — один из классов классических многоугольных чисел. Последовательность семиугольных чисел имеет вид :




































