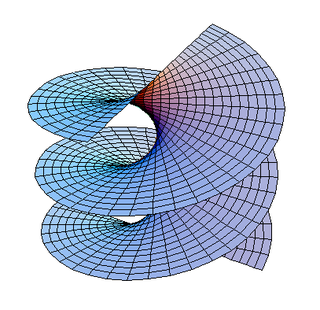
Гелико́ид — винтовая поверхность, описываемая параметрическими соотношениями


В теории узлов восьмёрка — это единственный узел с числом пересечений четыре. Это наименьшее возможное число пересечений после трилистника и тривиального узла. Восьмёрка является простым узлом. Впервые рассмотрен Листингом в 1847 году.

Фу́нкции Бе́сселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

Ма́трицей поворо́та называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Параболические координаты — ортогональная система координат на плоскости, в которой координатные линии являются конфокальными параболами. Трёхмерный вариант этой системы координат получается при вращении парабол вокруг их оси симметрии.
Правило дифференцирования сложной функции позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных.

Суперквадрики — семейство геометрических поверхностей, определяемых уравнением эллипсоида и других поверхностей второго порядка, где показатели степени 2 заменены произвольным числом. Их можно считать трёхмерными аналогами кривых Ламе (суперэллипсов).

Поверхность Шерка является примером минимальной поверхности. Шерк описал две полные вложенные минимальные поверхности в 1834 году. Его первая поверхность является дважды периодической поверхностью, а вторая — просто периодической. Они были третьим нетривиальным примером минимальных поверхностей. Две поверхности сопряжены друг другу.

Минимальная поверхность Бура — двухмерная минимальная поверхность, вложенная с самопересечениями в трёхмерное евклидово пространство. Поверхность названа именем Эдмонда Бура, работа которого о минимальных поверхностях получила в 1861 году математический приз Французской академии наук.

В дифференциальной геометрии Минимальная поверхность Каталана — это минимальная поверхность, которую впервые исследовал Эжен Шарль Каталан в 1855 г..
Минимальные поверхности Шварца — это периодические минимальные поверхности, первоначально описанные Карлом Шварцем.

Трижды периодическая минимальная поверхность — это минимальная поверхность в  , являющаяся инвариантом по переносам в решётке ранга 3.
, являющаяся инвариантом по переносам в решётке ранга 3.
Функция, имеющая первообразную — функция, которая может быть получена в результате дифференцирования некоторой функции. Обычно термин употребляется по отношению к вещественнозначным функциям одного вещественного переменного, определённых на промежутке. Именно о таких функциях пойдёт речь далее в статье.
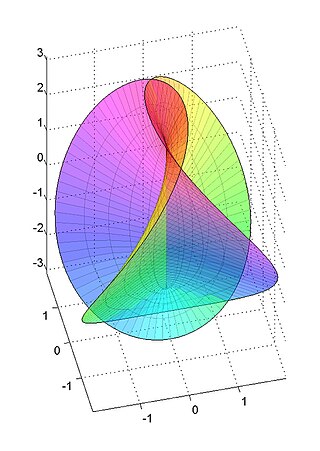
Поверхность Хеннеберга — неориентируемая минимальная поверхность, названная именем немецкого математика Лебрехта Хенненберга.
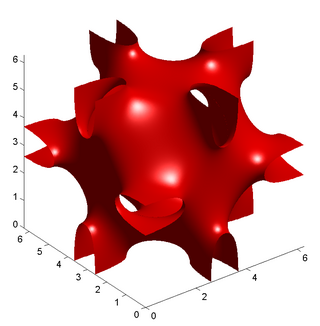
Поверхность Неовиуса — трижды периодическая минимальная поверхность, первоначально обнаруженная финским математиком Эдвардом Рудольфом Неовиусом.
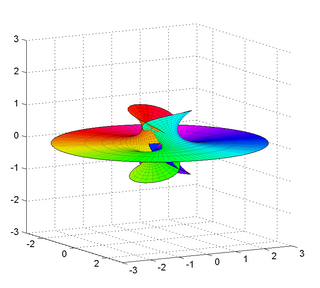
Поверхность Ричмонда — минимальная поверхность, впервые описанная английским математиком Гербертом Уильямом Ричмондом в 1904 году. Это семейство поверхностей с одним планарным концом и одним самопересекающимся концом как у поверхности Эннепера.

Гироид — бесконечно связанная трижды периодическая минимальная поверхность, открытая Аланом Шоэном в 1970 году

Ассоциированное семейство минимальной поверхности - является однопараметрическим семейством минимальных поверхностей, которые разделяют те же данные Вейерштрасса. То есть, если поверхность имеет представление


Параметризация Вейерштрасса — Эннепера минимальных поверхностей — классический раздел дифференциальной геометрии.

Кривые Эдвардса — семейство эллиптических кривых, изученных профессором математик Гарольдом Эдвардсом в 2007 году. Концепция эллиптических кривых над конечными полями широко используется в эллиптической криптографии. Первыми, кто исследовал преимущества эллиптической кривой в форме Эдвардса перед эллиптической кривой в форме Вейерштрасса, были Даниэль Бернстайн и Тани Ланге: они доработали оригинальную кривую Эдвардса, введя новый параметр кривой, и получили закон сложения точек для модифицированной кривой.
Эта страница основана на
статье Википедии.
Текст доступен на условиях лицензии
CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.

![{\displaystyle {\begin{aligned}(1/2)[&\sin(2x)\cos(y)\sin(z)\\+&\sin(2y)\cos(z)\sin(x)\\+&\sin(2z)\cos(x)\sin(y)]\\-&(1/2)[\cos(2x)\cos(2y)\\+&\cos(2y)\cos(2z)\\+&\cos(2z)\cos(2x)]+0{,}15=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfaf45bfd96123e4ce3c14b9b98062c0742fb027)



















