Линейный классификатор
Линейный классификатор — способ решения задач классификации, когда решение принимается на основании действия линейного оператора над входными данными. Класс задач, которые можно решать с помощью линейных классификаторов, обладают, соответственно, свойством линейной сепарабельности.
Определение
Пусть вектор из действительных чисел представляет собой входные данные, а на выходе классификатора вычисляется показатель y по формуле:
здесь - действительный вектор весов, а f - функция преобразования скалярного произведения. (Иными словами, вектор весов - ковариантный вектор или линейная форма отображения в R.) Значения весов вектора определяются в ходе машинного обучения на подготовленных образцах. Функция f обычно простая пороговая функция, отделяющая один класс объектов от другого. В более сложных случаях Функция f имеет смысл вероятности того или иного решения.
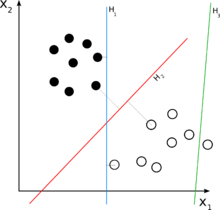
Операцию линейной классификации для двух классов можно себе представить как отображение объектов в многомерном пространстве на гиперплоскость, в которой те объекты, которые попали по одну сторону разделяющей линии, относятся к первому классу ("да"), а объекты по другую сторону - ко второму классу ("нет")).
Линейный классификатор используется когда важно проводить быстрые вычисления с большой скоростью. Он неплохо работает, когда входной вектор разрежен. Линейные классификаторы могут хорошо срабатывать в многомерном пространстве, например, для классификации документов по матрице встречаемости слов. В подобных случаях считается, что объекты хорошо регуляризируемы.
Генеративная и дискриминативная модели
Существует два подхода к определению параметров для линейного классификатора - генеративные или дискриминативные модели.[1][2]
Генеративная модель использует условное распределение . Например:
- Дискриминантный анализ (LDA) — предполагает нормальное распределение по Гауссу. [3]:117
- Наивный байесовский классификатор с Бернуллиевской моделью событий.
Дискриминативные модели стремятся улучшить качество выходных данных на наборе образцов для обучения. Например:
- Логистическая регрессия — стремление достичь максимального сходства через вектор of из предположения, что наблюдаемый набор образцов генерировался в виде биномиальной модели от выходных данных.
- Простой Перцептрон — алгоритм коррекции всех ошибок на входном наборе образцов.
- Метод опорных векторов — алгоритм расширения разделительной зоны в гиперплоскости решений между образцами входных данных.
Дискриминативные модели более точны, однако при неполной информации в данных легче использовать условное распределение.
Дискриминативное обучение
Обучение при использовании дискриминативных моделей строится через "Обучение с учителем" , то есть через процесс оптимизации выходных данных на заданных образцах для обучения. При этом определяется функция потерь, измеряющая несогласование между выходными данными и желаемыми результатами. Формально задача обучения (как оптимизации) записывается как: [4]
где
- w - искомый вектор весов классификатора,
- L(yi, wTxi) функция потерь (то есть, несоответствие между выходом классификатора и истинными значениями yi для i-го образца),
- R(w) - функция регуляризации, которая не позволяет параметрам выходить за разумные пределы (по причине переобучения),
- C - константа, определяемая пользователем алгоритма обучения для балансировки между регуляризацией и функцией потерь.
Наиболее популярны кусочно-линейная функция и логарифмическая (Перекрёстная энтропия) функции потерь. Если функция регуляризации R выпуклая, то ставится проблема выпуклой оптимизации[4]. Для решения этих задач используется много алгоритмов, в частности метод стохастического градиентного спуска, метод градиентного спуска, L-BFGS, метод координатного спуска и Метод Ньютона.[]
См. также
Примечания
- ↑ T. Mitchell, Generative and Discriminative Classifiers: Naive Bayes and Logistic Regression. Архивная копия от 24 февраля 2021 на Wayback Machine Draft Version, 2005
- ↑ A. Y. Ng and M. I. Jordan. On Discriminative vs. Generative Classifiers: A comparison of logistic regression and Naive Bayes. Архивная копия от 4 марта 2016 на Wayback Machine in NIPS 14, 2002.
- ↑ R.O. Duda, P.E. Hart, D.G. Stork, "Pattern Classification", Wiley, (2001). ISBN 0-471-05669-3
- ↑ 1 2 Guo-Xun Yuan; Chia-Hua Ho; Chih-Jen Lin. Recent Advances of Large-Scale Linear Classification (англ.) // Proc. IEEE[англ.] : journal. — 2012. — Vol. 100, no. 9.
Литература
- Y. Yang, X. Liu, "A re-examination of text categorization", Proc. ACM SIGIR Conference, pp. 42–49, (1999). paper @ citeseer
- R. Herbrich, "Learning Kernel Classifiers: Theory and Algorithms," MIT Press, (2001). ISBN 0-262-08306-X