Икосаэдрическая пирамида

Икосаэдрическая пирамида
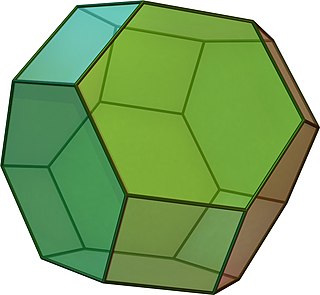
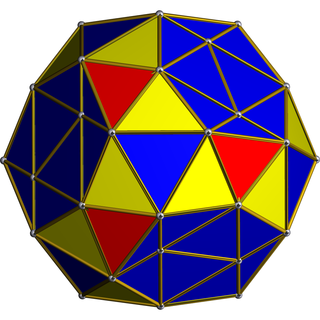
Диаграмма Шлегеля: проекция (перспектива) правильной икосаэдрической пирамиды в трёхмерное пространство
Тип	Многогранная пирамида[англ.]
Символ Шлефли	( ) ∨ {3,5}
Ячеек	21
Граней	50
Рёбер	42
Вершин	13
Двойственный политоп	Додекаэдрическая пирамида

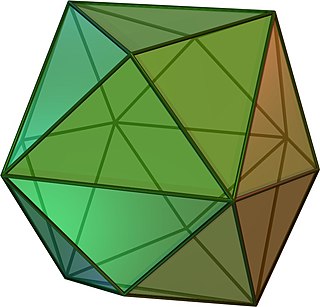
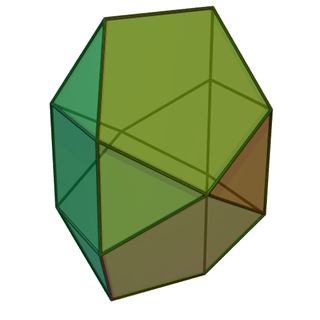
Икосаэдри́ческая пирами́да — четырёхмерный многогранник (многоячейник): многогранная пирамида^[англ.], имеющая основанием икосаэдр.

Ограничена 21 трёхмерной ячейкой — 20 тетраэдрами и 1 икосаэдром. Икосаэдрическая ячейка окружена всеми двадцатью тетраэдрическими; каждая тетраэдрическая ячейка окружена икосаэдрической и тремя тетраэдрическими.

Её 50 двумерных граней — треугольники. 20 граней разделяют икосаэдрическую и тетраэдрическую ячейки, остальные 30 — две тетраэдрических.

Имеет 42 ребра. На 30 рёбрах сходятся по три грани и по три ячейки (икосаэдрическая и две тетраэдрических), на остальных 12 — по пять граней и по пять ячеек (только тетраэдрические).

Имеет 13 вершин. В 12 вершинах сходятся по 6 рёбер, по 10 граней и по 6 ячеек (икосаэдрическая и пять тетраэдрических); в 1 вершине — 12 рёбер, 30 граней и все 20 тетраэдрических ячеек.

Если все рёбра икосаэдрической пирамиды имеют равную длину ${\displaystyle a}$, её грани являются одинаковыми правильными треугольниками. Четырёхмерный гиперобъём и трёхмерная гиперплощадь поверхности такой пирамиды выражаются соответственно как

${\displaystyle V_{4}={\frac {5}{96}}\left(1+{\sqrt {5}}\right)a^{4}\approx 0{,}1685452a^{4},}$

${\displaystyle S_{3}={\frac {5}{12}}\left(3+4{\sqrt {2}}+{\sqrt {5}}\right)a^{3}\approx 4{,}5387176a^{3}.}$

Высота пирамиды при этом будет равна

${\displaystyle H={\frac {1}{4}}\left({\sqrt {5}}-1\right)a\approx 0{,}3090170a,}$

радиус описанной гиперсферы (проходящей через все вершины многоячейника) —

${\displaystyle R={\frac {1}{2}}\left(1+{\sqrt {5}}\right)a\approx 1{,}6180340a,}$

радиус внешней полувписанной гиперсферы (касающейся всех рёбер в их серединах) —

${\displaystyle \rho _{1}={\frac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}\;a\approx 1{,}5388418a,}$

радиус внутренней полувписанной гиперсферы (касающейся всех граней в их центрах) —

${\displaystyle \rho _{2}={\frac {1}{6}}\left({\sqrt {15}}+3{\sqrt {3}}\right)a\approx 1{,}5115226a,}$

радиус вписанной гиперсферы (касающейся всех ячеек) —

${\displaystyle r={\frac {\left(4{\sqrt {2}}-5\right)\left(2+{\sqrt {5}}\right)-1}{12}}\;a\approx 0{,}1485399a.}$

Центр вписанной гиперсферы располагается внутри пирамиды, центры описанной и обеих полувписанных гиперсфер — в одной и той же точке вне пирамиды.

Такую пирамиду можно получить, взяв выпуклую оболочку любой вершины шестисотячейника и всех 12 соседних вершин, соединённых с ней ребром.

Угол между двумя смежными тетраэдрическими ячейками будет равен ${\displaystyle \arccos \left(-{\frac {1+3{\sqrt {5}}}{8}}\right)\approx 164{,}48^{\circ },}$ как и в шестисотячейнике. Угол между икосаэдрической ячейкой и любой тетраэдрической будет равен ${\displaystyle \arccos {\frac {\sqrt {7+3{\sqrt {5}}}}{4}}\approx 22{,}24^{\circ }.}$

Равногранную икосаэдрическую пирамиду с длиной ребра ${\displaystyle 2}$ можно разместить в декартовой системе координат так, чтобы её вершины имели координаты

• ${\displaystyle \left(0;\;\pm 1;\;\pm \Phi ;\;0\right),}$
• ${\displaystyle \left(\pm \Phi ;\;0;\;\pm 1;\;0\right),}$
• ${\displaystyle \left(\pm 1;\;\pm \Phi ;\;0;\;0\right),}$
• ${\displaystyle \left(0;\;0;\;0;\;\Phi ^{-1}\right),}$

где ${\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}$ — отношение золотого сечения.

• Richard Klitzing. Icosahedral pyramid